Content

• Steps
• Part 1 of 3: Finding the value of work in one dimension
• Part 2 of 3: Calculating Work Using Angular Force
• Part 3 of 3: Using Work Value
• Tips

In physics, the concept of "work" has a different definition than that which is used in everyday life. In particular, the term "work" is used when physical force causes an object to move. In general, if a powerful force makes an object move very far, then a lot of work is being done. And if the force is small or the object does not move very far, then only a little work. Strength can be calculated using the formula: Work = F × D × cosine (θ)where F = force (in Newtons), D = displacement (in meters), and θ = angle between the force vector and the direction of motion.

Steps

Part 1 of 3: Finding the value of work in one dimension

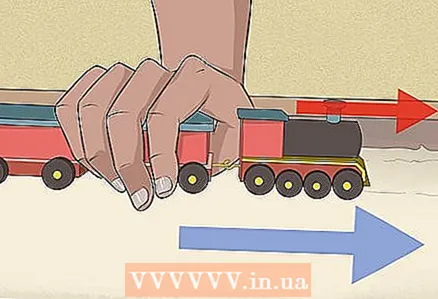1. 1 Find the direction of the force vector and the direction of movement. To get started, it is important to first determine in which direction the object is moving, as well as where the force is being applied from. Keep in mind that objects do not always move in accordance with the force applied to them - for example, if you pull a small cart by the handle, then you are applying a diagonal force (if you are taller than the cart) to move it forward. In this section, however, we will deal with situations in which the force (effort) and movement of an object have same direction. For information on how to find a job when these items not have the same direction, read below.
   • To make this process easy to understand, let's follow the example task. Let's say a toy carriage is pulled straight ahead by the train in front of it. In this case, the force vector and the direction of movement of the train indicate the same path - forward... In the next steps, we will use this information to help find the work done by the entity.
2. 2 Find the offset of the object. The first variable D, or offset, that we need for the work formula is usually easy to find. Displacement is simply the distance the force caused the object to move from its original position. In educational problems, this information is usually either given (known), or it can be derived (found) from other information in the problem. In real life, all you have to do to find the displacement is to measure the distance the objects are moving.
   • Note that distance units must be in meters in the formula to calculate the work.
   • In our toy train example, let's say we find the work done by the train as it passes along the track. If it starts at a certain point and stops at a place about 2 meters along the track, then we can use 2 meters for our "D" value in the formula.
3. 3 Find the force applied to the object. Next, find the amount of force that is used to move the object. This is a measure of the "strength" of the force - the greater its value, the stronger it pushes the object and the faster it accelerates its course. If the magnitude of the force is not provided, it can be derived from the mass and the acceleration of displacement (provided that there are no other conflicting forces acting on it) using the formula F = M × A.
   • Please note that the force units must be in Newtons to calculate the work formula.
   • In our example, let's say we don't know the magnitude of the force. However, let's assume that knowthat the toy train has a mass of 0.5 kg and that the force causes it to accelerate at a speed of 0.7 meters / second. In this case, we can find the value by multiplying M × A = 0.5 × 0.7 = 0.35 Newton.
4. 4 Multiply Strength × Distance. Once you know the amount of force acting on your object and the distance it was moved, the rest will be easy. Just multiply these two values ​​by each other to get the work value.
   • It's time to solve our example problem. With a force value of 0.35 Newton and a displacement value of 2 meters, our answer is a matter of simple multiplication: 0.35 × 2 = 0.7 Joules.
   • You may have noticed that the formula given in the introduction has an extra part to the formula: cosine (θ). As discussed above, in this example, the force and direction of movement are applied in the same direction. This means that the angle between them is 0. Since cosine (0) = 1, then we should not include it - we just multiply by 1.
5. 5 Indicate the answer in Joules. In physics, the values ​​of work (and several other quantities) are almost always given in a unit of measurement called the joule. One joule is defined as 1 Newton of force applied per meter, or in other words, 1 Newton × meter. This makes sense - since you are multiplying distance by force, it makes sense that the answer you get will have a unit of measurement equal to the unit of your force multiplied by your distance.
   • Note that Joule also has an alternative definition of 1 Watt of power emitted per second. Read below for a more detailed discussion of power and how it relates to performance.

Part 2 of 3: Calculating Work Using Angular Force

1. 1 Find strength and displacement as usual. Above, we dealt with a problem in which an object moves in the same direction as the force that is applied to it. In fact, this is not always the case. In cases where the force and motion of an object are in two different directions, the difference between these two directions must also be factored into the equation to obtain an accurate result. First, find the amount of force and displacement of the object, as you usually do.
   • Let's take a look at another example of a problem. In this case, suppose we are pulling the toy train forward, as in the example problem above, but this time we are actually pulling upwards at a diagonal angle.In the next step, we will take this into account, but for now we will stick to the basics: the movement of the train and the magnitude of the force acting on it. For our purposes, let's say the force has the magnitude 10 Newton and that he drove the same 2 meters forward as before.
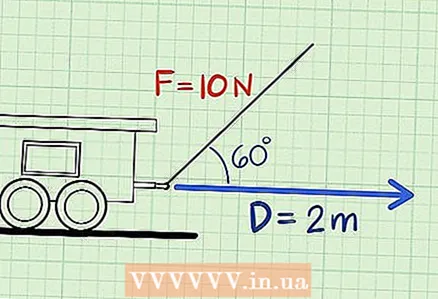2. 2 Find the angle between the force vector and the displacement. Unlike the examples above with a force that is in a different direction than the movement of the object, you need to find the difference between the two directions in terms of the angle between them. If this information is not provided to you, then you may need to measure the angle yourself or derive it from other information in the problem.
   • In our example problem, assume that the force that is applied is approximately 60 above the horizontal plane. If the train is still moving straight ahead (that is, horizontally), then the angle between the force and motion vector of the train will be 60.
3. 3 Multiply Force × Distance × Cosine (θ). Once you know the displacement of an object, the amount of force acting on it, and the angle between the force vector and its motion, the decision is almost as easy as without taking the angle into account. Just take the cosine of an angle (this may require a scientific calculator) and multiply it by force and displacement to find the answer to your problem in Joules.
   • Let's solve an example of our problem. Using the calculator, we find that cosine 60 is 1/2. Including this in the formula, we can solve the problem as follows: 10 Newtons × 2 meters × 1/2 = 10 Joules.

Part 3 of 3: Using Work Value

1. 1 Modify the formula to find distance, strength, or angle. The work formula above is not simply useful for finding work - it is also valuable for finding any variables in an equation when you already know the meaning of work. In these cases, simply highlight the variable you are looking for and solve the equation according to the basic rules of algebra.
   • For example, suppose we know that our train is being pulled with a force of 20 Newtons at a diagonal angle of more than 5 meters of track to do 86.6 Joules of work. However, we do not know the angle of the force vector. To find the angle, we simply select this variable and solve the equation as follows:

     86.6 = 20 × 5 × Cosine (θ)

     86.6 / 100 = Cosine (θ)

     Arccos (0.866) = θ = 30

2. 2 Divide by the time spent on the move to find the power. In physics, work is closely related to another type of measurement called "power". Power is simply a way of quantifying the amount of speed at which work is done on a particular system over a long period of time. Thus, to find the power, all you have to do is divide the work used to move the object by the time it takes to complete the move. Power measurements are indicated in units of W (which are equal to Joule / second).
   • For example, for the example problem in the above step, suppose it took 12 seconds to move the train 5 meters. In this case, all you have to do is divide the work done to move it 5 meters (86.6 J) by 12 seconds to find the answer for calculating the power: 86.6 / 12 = '7.22 Watt.
3. 3 Use the TME formula_i + W_nc = TME_fto find the mechanical energy in the system. The work can also be used to find the amount of energy contained in the system. In the above formula TME_i = initial total mechanical energy in the TME system_f = final total mechanical energy in the system and W_nc = work done in communication systems due to non-conservative forces .. In this formula, if a force is applied in the direction of movement, then it is positive, and if it presses on (against) it, then it is negative. Note that both energy variables can be found by the formula (½) mv, where m = mass and V = volume.
   • For example, for the example of the problem two steps above, suppose that the train initially had a total mechanical energy of 100 J. Since the force in the problem pulls the train in the direction it has already passed, it is positive. In this case, the final energy of the train is TME_i + W_nc = 100 + 86.6 = 186.6 J.
   • Note that non-conservative forces are forces whose power to affect the acceleration of an object depends on the path traveled by the object.Friction is a good example - an object pushed along a short, straight path will feel the effects of friction for a short time, while an object pushed along a long, winding path to the same final location will experience more friction overall.

Tips

• If you succeed in solving the problem, then smile and be happy for yourself!
• Practice solving as many problems as possible, this will ensure complete understanding.
• Keep practicing and try again if you fail the first time.
• Study the following points about work:
  • The work done by force can be either positive or negative. (In this sense, the terms "positive or negative" carry their mathematical meaning, and their usual meaning).
  • The work done is negative when the force acts in the opposite direction to the displacement.
  • The work done is positive when the force acts in the direction of travel.