Content

• Steps
• Advice
• Warning
• What you need

In chemistry, "partial pressure" is the pressure of each gas in the mixture of gases acting on the surrounding environment, such as a sample gas tank in a laboratory, a diver's gas tank, or the surrounding space. atmosphere. You can calculate the pressure of each gas in the mixture if you know its mass, volume, and temperature. You then add the partial pressures to get the total pressure of the gas mixture, or you find the total pressure first and then find the partial pressure.

Steps

Part 1 of 3: Understanding gas properties

1. 

   Treat each gas as an "ideal" gas. In chemistry, the ideal gas is one that interacts with other gases without being attracted to their molecules. Gas molecules can collide with each other and bounce off like billiard balls without deformation.
   • The pressure of an ideal gas increases as it is compressed into a smaller space and decreases as it disperses into a larger space. This relationship is known as Boyle's Law (named after scientist Robert Boyle). The math formula shows that this relationship is k = P x V, or more simply k = PV, where k is a constant relationship between pressure and volume, P is pressure and V is a body. area.
   • The problem can be given the pressure in one of many different units. In which pascal (Pa) is defined as the force of a newton acting on a square meter. Another unit is atmosphere (atm), which is defined as the pressure of the earth's atmosphere at an altitude equal to sea level. The pressure of 1 atm is 101,325 Pa.
   • The temperature of the ideal gas increases as the volume increases and decreases as the volume decreases. This relationship is known as Charles's Law (named after the scientist Jacques Charles). The mathematical formula for this is k = V / T, where k is the constant relationship between volume and temperature, V is volume, and T is temperature.
   • The temperature of the gas in this equation is calculated in degrees Kelvin, and degrees Kelvin by adding degrees Celsius by 273.
   • These two relationships can be combined into a single equation: k = PV / T, or they can be written as PV = kT.

2. 

   
   
   Defines the mass unit used to measure gas. The gas has both mass and volume. Volumes are usually measured in liters (l), but there are two masses of gas.
   • Conventional masses are measured in grams or, if the mass is large enough, in kilograms.
   • Since most gases are often so light, they are also measured with another form of mass called a molar mass or molar mass. Molar mass is defined as the sum of the atomic mass of each atom in the composition of the gas, with the mass of each atom compared with the mass of carbon (value 12).
   • Since atoms and molecules are so small to calculate, the mass of the gas is defined in moles. The number of moles present in a gas quantity can be calculated by dividing the mass of the gas by its molar mass, and is denoted by the letter n.
   • We can replace any constant k in the gas equation with the product of n, the number of moles, and a new constant R. We now have the equation nR = PV / T or PV = nRT.
   • The R value depends on the unit used to measure the pressure, volume and temperature of the gas. If volume is in liters, temperature in degrees Kelvin, and pressure in atmosphere, this is 0.0821 L atm / K mol. You can also write 0.0821 L atm K mol to avoid having to use the slash of the division in units of measure.

3. 

   
   
   Dalton's law of partial pressure. This law was proposed by chemist and physicist John Dalton, who presented the concept of a chemical element made of atoms for the first time. Dalton's Law states that the total pressure of the gas mixture is the total pressure of each gas in the mixture.
   • Dalton's law can be written into the equation after P_total = P₁ + P₂ + P₃ ... with the amount of pressure P equal to the number of gases in the mixture.
   • The Dalton Law equation can be developed when dealing with gases whose partial pressure is unknown, but whose volume and temperature are known. The partial pressure of a gas is the pressure exerted by the same amount of gas in a tank containing only it alone.
   • For each partial pressure, we can rewrite the ideal gas equation PV = nRT to a form only P on the left side of the equal sign. Thus, we have to divide the two sides by V: PV / V = ​​nRT / V. The two V's on the left-hand side are eliminated, leaving P = nRT / V at the end.
   • Then replace this formula with each letter P on the right side of the partial pressure equation: P_total = (nRT / V) ₁ + (nRT / V) ₂ + (nRT / V) ₃ …
   advertisement

Part 2 of 3: Calculate partial pressure, then total pressure

1. 

   
   
   
   
   Determine the partial pressure equations for the problems given. To illustrate this calculation, suppose we have a 2 liter bottle containing 3 gases: nitrogen (N₂), oxygen (O₂), and carbon dioxide (CO₂). Each gas has 10 g, and the temperature of each gas in the cylinder is 37 degrees Celsius. We need to find the partial pressure of each gas and the total pressure of the gas mixture acting on the cylinder.
   • The partial pressure equation is written as follows P_total = P_Nitrogen + P_oxygen + P_{carbon dioxide}.
   • Since we are looking for the pressure of each gas, we know the volume, the temperature, and we can find the mole number of each gas based on their mass, this equation is rewritten to: P_total = (nRT / V) _Nitrogen + (nRT / V) _oxygen + (nRT / V) _{carbon dioxide}

2. 

   
   
   Convert the temperature to degrees Kelvin. The temperature of the gases is 37 degrees Celsius so we add 37 plus 273 to get 310 degrees K.

3. 

   Find the number of moles of each gas in the bottle. The number of moles of gas is the mass of the gas divided by its molar mass, where the molar mass is the total mass of each of the atoms that make up the substance.
   • For the first gas, nitrogen has the molecular formula (N₂), each atom has a mass 14. Since the nitrogen molecule has two atoms, we must multiply 14 by 2 to get a molecular weight of nitrogen 28, then divide the mass in grams by 10g. give 28 to get the number of moles, round the result to approximately 0.4 moles of nitrogen gas.
   • For the second gas, oxygen has the molecular formula (O₂), each atom has a mass of 16. The oxygen molecule also has two atoms, we must multiply 16 by 2 to get an oxygen molecule mass of 32. Dividing 10g by 32 gives an approximate result 0.3 mole of oxygen in the bottle.
   • A third gas is the formula carbon dioxide (CO₂), there are 3 atoms: one carbon atom with mass 12, two oxygen atoms with each atom of mass 16. We add the mass of three atoms: 12 + 16 + 16 = 44 is mass molecule. Dividing 10g by 44 gives approximately 0.2 moles of carbon dioxide.

4. 

   
   
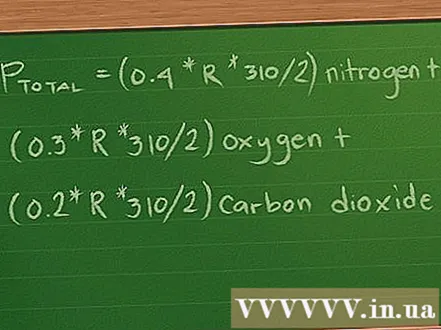
   Plug the values ​​for mol, volume, and temperature into the equation. Now the equation looks like this: P_total = (0.4 * R * 310/2) _Nitrogen + (0,3 * R * 310/2) _oxygen + (0.2 * R * 310/2) _{carbon dioxide}.
   • For simplicity we omit the unit of measure for the values. These units will be destroyed after you solve the equation, leaving only the unit of measure of the result in the pressure.

5. 

   Replace the value of the constant R. We will work out the results of the partial pressure and the total pressure in atmosphere, so we will use an R value of 0.0821 L atm / K mol. Putting this value into the equation yields P_total =(0,4 * 0,0821 * 310/2) _Nitrogen + (0,3 *0,0821 * 310/2) _oxygen + (0,2 * 0,0821 * 310/2) _{carbon dioxide}.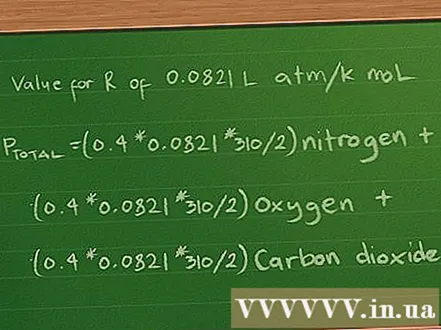

6. 

   Calculate the partial pressure of each gas. Now that we've plugged in our values, the next thing to do is solve it.
   • For the partial pressure of nitrogen, multiply 0.4 mol by the constant 0.0821 and the temperature 310 degrees K, then divide by 2 liters: 0.4 * 0.0821 * 310/2 = 5.09 atm (approx).
   • For the partial pressure of oxygen, multiply 0.3 mol by the constant 0.0821 and the temperature 310 degrees K, then divide by 2 liters: 0.3 * 0.0821 * 310/2 = 3.82 atm (approx.).
   • For the partial pressure of the carbon dioxide, multiply 0.2 mol by the constant 0.0821 and the temperature 310 degrees K, then divide by 2 liters: 0.2 * 0.0821 * 310/2 = 2.54 atm (approx).
   • Now add up these pressures to find the total pressure: P_total = 5.09 + 3.82 + 2.54 = 11.45 atm (approx).
   advertisement

Part 3 of 3: Calculate total pressure, then partial pressure

1. 

   Determine the partial pressure equation as above. Again, suppose we have a 2 liter bottle that contains 3 gases: nitrogen (N₂), oxygen (O₂), and carbon dioxide (CO₂). Each gas has 10 g, and the temperature of each gas in the cylinder is 37 degrees Celsius.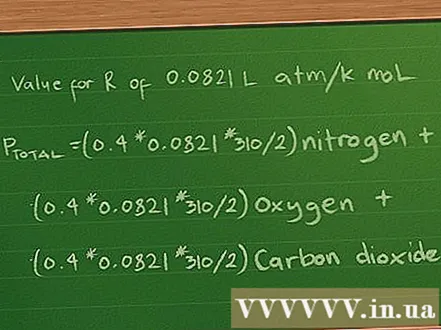
   • The Kelvin temperature is still 310 degrees, and as before, we have approximately 0.4 mol nitrogen, 0.3 mol oxygen and 0.2 mole carbon dioxide.
   • Similarly, we will calculate the results under atmosphere so we will use an R value of 0.0821 L atm / K mol.
   • At this point the partial pressure equation remains: P_total =(0,4 * 0,0821 * 310/2) _Nitrogen + (0,3 *0,0821 * 310/2) _oxygen + (0,2 * 0,0821 * 310/2) _{carbon dioxide}.

2. 

   Add the number of moles of each gas in the cylinder to find the total moles of the gas mixture. Since the volumes and temperatures of the gases in the cylinder are the same, and the molecular mass per gas is also multiplied by the same constant, we can use the distributive property of mathematics to rewrite the equation. Process is P_total = (0,4 + 0,3 + 0,2) * 0,0821 * 310/2.
   • Add 0.4 + 0.3 + 0.2 = 0.9 moles of gas mixture. Equation is further reduced to P_total = 0,9 * 0,0821 * 310/2.

3. 

   Find the total pressure of the gas mixture. Take 0.9 * 0.0821 * 310/2 = 11.45 mol (approx.).

4. 

   Find the proportion of each gas that makes up the mixture. You divide the number of moles per gas by the total moles of the gas mixture.
   • We have 0.4 moles of nitrogen so we take 0.4 / 0.9 = 0.44 (44%) in the gas mixture (approx.).
   • We have 0.3 mole of oxygen so we take 0.3 / 0.9 = 0.33 (33%) in the gas mixture (approx).
   • We have 0.2 mole of carbon dioxide so we take 0.2 / 0.9 = 0.22 (22%) in the gas mixture (approx.).
   • Although the approximate percentages above add up to only 0.99, in reality, the decimals keep repeating, with the sum being a series of 9s after the comma. By definition this is equivalent to 1 or 100 percent.

5. 

   Multiply the ratio of mass per gas by total pressure to find the partial pressure.
   • Take 0.44 * 11.45 = 5.04 atm (approx).
   • Take 0.33 * 11.45 = 3.78 atm (approx.).
   • Take 0.22 * 11.45 = 2.52 atm (approx.).
   advertisement

Advice

• You will notice a slight discrepancy between the partial pressure calculation and the partial pressure calculation first and the partial pressure calculation. Remember that the calculated values ​​are only approximate numbers since we round to 1 or 2 numbers after commas to make them simpler.If we use a calculator to perform calculations without rounding, the deviation between these two methods will be even smaller, not even.

Warning

• For divers, knowledge of the gas partial pressure is especially important as it is related to their life. An oxygen partial pressure that is too low can cause loss of consciousness or death, while too high a nitrogen or oxygen partial pressure can cause poisoning.

What you need

• Laptop
• Reference book for atomic mass / molar mass