Content

• Steps
• Advice
• Warning
• What you need

The vertex of a quadratic or parabolic equation is the highest or lowest point in that equation. It lies on the plane of symmetry of the whole parabola; Any point on the left side of the parabola is a full reflection of the point to the right. If you want to find the vertex of a quadratic equation, you can use the vertex formula, or the squared complement.

Steps

Method 1 of 2: Use the Find Vertex Formula

1. 

   Determine the values ​​a, b, and c. In the quadratic equation, the coefficient of x = a, coefficient of x = b, and the constant = c. Suppose we have the following equation: y = x + 9x + 18. In this example, a = 1, b = 9, and c = 18.

2. 

   
   
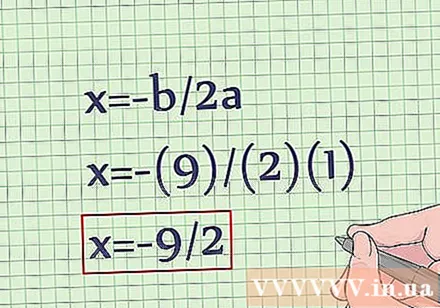
   Use the vertex formula to find the x value of the parabolic vertex. The vertex is also the symmetry axis of the equation. The formula for finding the x value of the vertex of a quadratic equation is x = -b / 2a. Replace the corresponding values ​​to find x:
   • x = -b / 2a
   • x = - (9) / (2) (1)
   • x = -9 / 2

3. 

   
   
   Substitute x into the original equation to find y. Once you know the x value, just plug it into the original formula and you'll get y. You can consider the vertex formula of a quadratic function as (x, y) = . This means that to find the y value, you must find the x value based on the given formula and then insert it into the equation. Here's how:
   • y = x + 9x + 18
   • y = (-9/2) + 9 (-9/2) +18
   • y = 81/4 -81/2 + 18
   • y = 81/4 -162/4 + 72/4
   • y = (81 - 162 + 72) / 4
   • y = -9/4

4. 

   
   
   Write values ​​for x and y in coordinate order. Now that you know x = -9/2, and y = -9/4, just write them in the coordinate order: (-9/2, -9/4). The vertex of this quadratic equation is (-9/2, -9/4). If you plot this parabola, this will be the base of the parabola, since the coefficient of x is positive. advertisement

Method 2 of 2: Squared Compensation

1. 

   Write down the equation. The squared complement is another way to find the vertex of a quadratic equation. With this method, you can immediately find the coordinates of x and y instead of finding x first and then replacing x in the original equation to find y. Suppose we have the following quadratic equation: x + 4x + 1 = 0.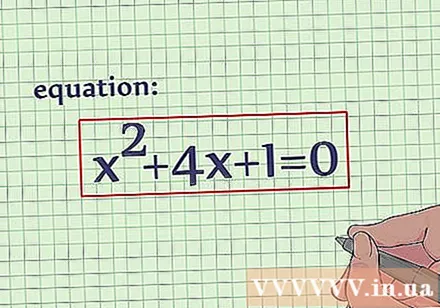

2. 

   Divide each term by the coefficient of x. In this example, the coefficient of x is 1, so you can skip this step.

3. 

   Move the constant to the right of the equation. The constant is a constant term. In this example, the constant equals "1". Switch 1 to the other side of the equation by subtracting both sides by 1. How to do it:
   • x + 4x + 1 = 0
   • x + 4x + 1 -1 = 0 - 1
   • x + 4x = - 1

4. 

   Compensate the square on the left side of the equation. To do this, simply find (b / 2) and add the results to the two sides of the equation. Replace "4" for b, because "4x" is the term b of this equation.
   • (4/2) = 2 = 4. Now add 4 to both sides of the equation, we have:
     • x + 4x + 4 = -1 + 4
     • x + 4x + 4 = 3

5. 

   Analyze the left side of the equation into a factor. You can see that x + 4x + 4 is a perfect square number. It can be rewritten as (x + 2) = 3

6. 

   Use this format to find x and y coordinates. You can find the x coordinate by setting (x + 2) equal to 0. When (x + 2) = 0, x will be -2, then your x coordinate is -2. The y coordinate is a constant on the other side of the equation. So y = 3. You can also shorten it by left the sign of the number inside the brackets to get the x coordinate. So the vertex of the equation x + 4x + 1 = (-2, 3) Advertising

Advice

• Correctly determine a, b, and c.
• Math operations must follow order to get the correct result.

Warning

• Check out your results!
• Make sure that a, b, and c are correct - otherwise, the answer will be wrong.
• Don't worry - this calculation takes practice.

What you need

• Book of graph paper or calculator screen
• Computer