Factor quadratic equations

Video: How To Solve Quadratic Equations By Factoring - Quick & Simple!

Content

To step
The beginning
Method 1 of 6: Trial and Error
Method 2 of 6: Decomposition
Method 3 of 6: Triple Play
Method 4 of 6: The difference between two squares
Method 5 of 6: The ABC formula
Method 6 of 6: Using a calculator
Tips
Warnings
Necessities

A polynomial contains a variable (x) to a power, and several terms and / or constants. To factor a polynomial, you will have to break the expression into smaller expressions that are multiplied together. This does require a certain level of math and can therefore be difficult to understand if you are not that far yet.

To step

The beginning

The equation. The standard format for a quadratic equation is:

ax + bx + c = 0
Start by arranging the terms in your equation from the highest to the lowest power. For example, take:

6 + 6x + 13x = 0
We're going to reorder this expression so it becomes easier to work with - simply by moving the terms:

6x + 13x + 6 = 0
Find the factors using one of the methods below. Factoring the polynomial will result in two smaller expressions that can be multiplied together to get the original polynomial:

6x + 13x + 6 = (2x + 3) (3x + 2)
In this example, (2x +3) and (3x + 2) are factors from the original expression, 6x + 13x + 6.
Check your work! Multiply the factors you found. Combine the same terms and you are done. Start with:

(2x + 3) (3x + 2)
Let's test this, multiplying the terms using EBBL (first - outer - inner - last), which gives us:

6x + 4x + 9x + 6
Now we add 4x and 9x because they are equal terms. We know the factors are correct because we get back the equation we started with:

6x + 13x + 6

Method 1 of 6: Trial and Error

If you have a fairly simple polynomial, you might be able to see what the factors are right away. For example, after some practice, many mathematicians are able to see the expression 4x + 4x + 1 has the factors (2x + 1) and (2x + 1) simply because they have seen this so many times. (Obviously, this won't be that easy with more complicated polynomials.) For this example, let's take a less standard expression:

3x + 2x - 8

Write down the factors of the a term and the c term. Use the format ax + bx + c = 0, recognize the a and c terms and note which factors there are. For 3x + 2x - 8, this means:

a = 3 and has 1 pair of factors: 1 * 3
c = -8 and this has 4 pairs of factors: -2 * 4, -4 * 2, -8 * 1, and -1 * 8.
Write down two pairs of parentheses with an empty space. Here you enter the constants of each expression:

(x) (x)
Fill the space before the x's with a number of possible factors of the a value. For the a term in our example, 3x, there is only 1 possibility:

(3x) (1x)
Fill in the 2 spaces after the x's with a few factors for the constants. Suppose we choose 8 and 1. Enter this:

(3x8)(X1)
Determine which signs (plus or minus) should be between the x variables and the numbers. Depending on the characters of the original expression, it is possible to find out what the characters of the constants should be. Let's take the two constants of the two factors h and k to mention:

If ax + bx + c then (x + h) (x + k)
If ax - bx - c or ax + bx - c then (x - h) (x + k)
If ax - bx + c then (x - h) (x - k)
In our example, 3x + 2x - 8, the sign is: (x - h) (x + k), which gives us the following two factors:

(3x + 8) and (x - 1)
Test your choice with the first-outer-inner-last multiplication. A quick first test to see if the middle term is at least the correct value. If not, then you probably have the wrong one c factors chosen. Let's test the answer:

(3x + 8) (x - 1)
By multiplication we get:

3x - 3x + 8x - 8
Simplify this expression by adding the like terms (-3x) and (8x), and we get:

3x - 3x + 8x - 8 = 3x + 5x - 8
We now know that we took the wrong factors:

3x + 5x - 8 ≠ 3x + 2x - 8
Switch your choices as needed. In our example, let's try 2 and 4, instead of 1 and 8:

(3x + 2) (x - 4)
Now our c term equal to -8, but the outer / inner product of (3x * -4) and (2 * x) is -12x and 2x, which is not the correct b term or + 2x.

-12x + 2x = 10x
10x ≠ 2x
Reverse the order if necessary. Let's try to flip 2 and 4:

(3x + 4) (x - 2)
Now our c term (4 * 2 = 8) and still okay, but the outer / inner products are -6x and 4x. When we combine these we get:

-6x + 4x = 2x
2x ≠ -2x We are now getting pretty close to 2x where we want to be, but the sign is not correct yet.
Double check your characters if necessary. We keep this order, but swap it with the minus sign:

(3x - 4) (x + 2)
Now the c term still okay, and the outer / inner products are now (6x) and (-4x). Because:

6x - 4x = 2x
2x = 2x We now see the positive 2x back from the original problem. These must be the right factors.

Method 2 of 6: Decomposition

This method gives all possible factors of it a and c terms and uses them to find out which factors are correct. If the numbers are very large, or the guesswork of other methods is going to take too long, use this way. An example:

6x + 13x + 6

Multiply the a term with the c term. In this example, a is 6 and c is also 6.

6 * 6 = 36
Find the b term by factorization and testing. We are looking for 2 numbers that are factors of a * c , and together the b term (13).

4 * 9 = 36
4 + 9 = 13
Substitute the two numbers you get in your equation as the sum of the b term. Let's k and h to represent the 2 numbers we have, take 4 and 9:

ax + kx + hx + c
6x + 4x + 9x + 6
Factor the polynomial by grouping. Organize the equation so that you can separate the greatest common divisor of the first two terms and the last two terms. Both factors should be the same. Add the GGDs together and place them in brackets, next to the factors; as a result you get the two factors:

6x + 4x + 9x + 6
2x (3x + 2) + 3 (3x + 2)
(2x + 3) (3x + 2)

Method 3 of 6: Triple Play

Similar to the decomposition method. The "triple play" method examines the possible factors of the product of a and c and use it to find out what b must be. Take the equation as an example:

8x + 10x + 2

Multiply the a term with the c term. As with the decomposition method, we use this to determine the candidates for the b term. In this example: a is 8 and c is 2.

8 * 2 = 16
Find the 2 numbers with this number as the product and with a sum equal to the b term. This step is the same as the decomposition method - we test candidates for the constants. The product of the a and c terms is 16, and the c term is 10:

2 * 8 = 16
8 + 2 = 10
Take these 2 numbers and substitute them in the "triple play" formula. Take the 2 numbers from the previous step - let's get them h and k call them - and put them in the expression:

((ax + h) (ax + k)) / a

With this we get:

((8x + 8) (8x + 2)) / 8
See which of the two terms in the denominator can be fully divided by a. In this example, we're looking at whether (8x + 8) or (8x + 2) can be divided by 8. (8x + 8) is divisible by 8, so we divide this term by a and we leave the other unaffected.

(8x + 8) = 8 (x + 1)
The term we have kept here is the one that remains after dividing by the a term: (x + 1)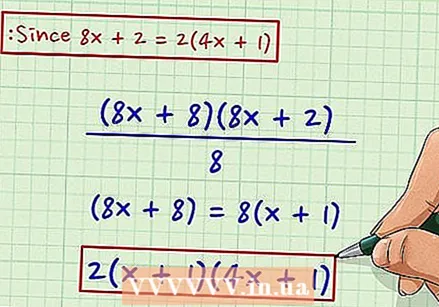
Take the greatest common divisor (gcd) from either or both terms, if possible. In this example, we see that the second term has gcd of 2, because 8x + 2 = 2 (4x + 1). Combine this answer with the term you discovered in the previous step. These are the factors of your comparison.

2 (x + 1) (4x + 1)

Method 4 of 6: The difference between two squares

You can recognize some coefficients in a polynomial as "squares", or also as the product of 2 identical numbers. By figuring out which squares are, you may be able to factor the polynomials much faster. We take the equation:

27x - 12 = 0

Remove the gcd from the equation, if possible. In this case we see that 27 and 12 are both divisible by 3, so we can place them separately:

27x - 12 = 3 (9x - 4)
Determine whether the coefficients of your equation are squares. To use this method it is necessary to determine the root of the terms. (Note that we have omitted the minus signs - since these numbers are squares, they may be the product of 2 negative numbers)

9x = 3x * 3x and 4 = 2 * 2
You can now write out the factors using the square root you determined. We take the a and c values from the previous step: a = 9 and c = 4, so the roots of this are: - √a = 3 and √c = 2. These are the coefficients of the factorized expressions:

27x - 12 = 3 (9x - 4) = 3 (3x + 2) (3x - 2)

Method 5 of 6: The ABC formula

If nothing seems to work and you can't solve the equation, use the abc formula. Take the following example:

x + 4x + 1 = 0

Enter the corresponding values in the abc formula:

x = -b ± √ (b - 4ac)
---------------------
2a
We now get the expression:

x = -4 ± √ (4 - 4 • 1 • 1) / 2
Solve for x. You should now get 2 values for x. These are:

x = -2 + √ (3) or x = -2 - √ (3)
Use the values of x to determine the factors. Enter the x values obtained in the two equations as constants. These are your factors. If we answer the two h and k we write down the two factors as follows:

(x - h) (x - k)
In this case, the final answer is:

(x - (-2 + √ (3)) (x - (-2 - √ (3)) = (x + 2 - √ (3)) (x + 2 + √ (3))

Method 6 of 6: Using a calculator

If it is allowed (or compulsory) to use a graphing calculator, this makes factoring a lot easier, especially for exams and exams. The following instructions are for a TI graphing calculator. We use the equation from the example:

y = x - x - 2

Enter the equation into your calculator. You will be using the equation solver, also known as the [Y =] screen.
Graph the equation with the calculator. Once you have entered the equation, press [GRAPH] - you should now see a curved line, a parabola as a graphical representation of your equation (and it is a parabola, because we are dealing with a polynomial).
Find where the parabola intersects with the x axis. Since a quadratic equation is traditionally written as ax + bx + c = 0, these are the two x values that make the equation equal to zero:

(-1, 0), (2 , 0)
x = -1, x = 2
- If you cannot see where the parabola intersects with the x-axis, press [2nd] and then [TRACE]. Press [2] or select "zero". Move the cursor to the left of an intersection point and press [ENTER]. Move the cursor to the right of an intersection and press [ENTER]. Move the cursor as close to the intersection point as possible and press [ENTER]. The calculator will indicate the x value. Do this for the other intersection as well.
Enter the x values you obtained into the two factored expressions. If we take the two x values h and k as a term, the expression we use looks like this:

(x - h) (x - k) = 0
So our two factors then become:

(x - (-1)) (x - 2) = (x + 1) (x - 2)

Tips

If you have factored the polynomial with the abc formula, and your answer contains roots, you can convert the x values to fractions to check them.
If a term has no coefficient in front of it, then the coefficient is equal to 1, eg x = 1x.
If you have a TI-84 calculator, there is a program called SOLVER that can solve a quadratic equation for you. It also solves higher degree polynomials.
After a lot of practice, you will eventually be able to solve polynomials by heart. But to be on the safe side, it is better to always write them out.
If a term does not exist, the coefficient is zero. Then it can be useful to rewrite the equation. E.g. x + 6 = x + 0x + 6.

Warnings

If you are learning this concept in math class, pay attention to what the teacher is explaining and don't just use your own favorite method. You may be asked to use a specific method for a test, or graphing calculators may not be allowed.