Content

• To step
• Method 1 of 4: Determine the weight
• Method 2 of 4: Determine the zero point
• Method 3 of 4: Determine the center of gravity
• Method 4 of 4: Check your answer
• Tips
• Warnings

The center of gravity (the center of mass) is the center of an object's weight distribution - the point where gravity acts on that object. This is the point where the object is in perfect balance, regardless of how the object has rotated or rotated around that point. If you want to know how to calculate the center of gravity of an object, you need the weight of the object and all the objects on it. Then you determine a zero point and process the known quantities in the equation to calculate the center of gravity of an object or system. If you want to know how to calculate the center of gravity, follow the steps below.

To step

Method 1 of 4: Determine the weight

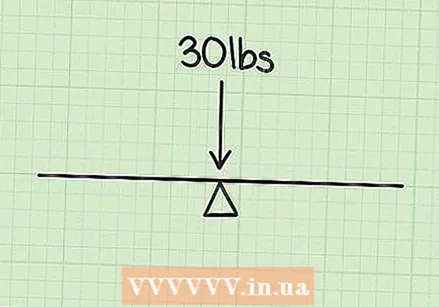1. Calculate the weight of the object. When calculating the center of gravity, you will first have to find out the weight of the object. Let's say you want to calculate the weight of a seesaw with a mass of 30 kilos. Since it is a symmetrical object, its center of gravity will be exactly in the middle (when no one is sitting on it). But when people of different masses are on the seesaw, the problem becomes a bit more complicated.
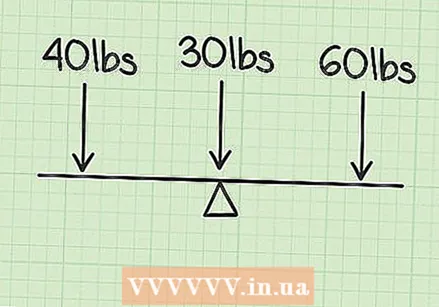2. Calculate the extra weights. To determine the center of gravity of the seesaw with two children on it, you will have to determine the individual weight of each child. The first child has a mass of 40 kilos and the second child is 60 kilos.

Method 2 of 4: Determine the zero point

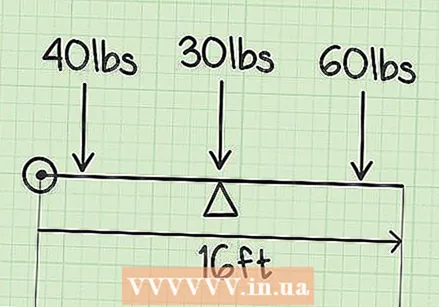1. Choose a zero point. The zero point is any starting point on one side of the seesaw. You can place the zero point on one side of the seesaw or on the other. Let's say the seesaw is 6 meters long. Let's place the zero point on the left side of the seesaw, close to the first child.
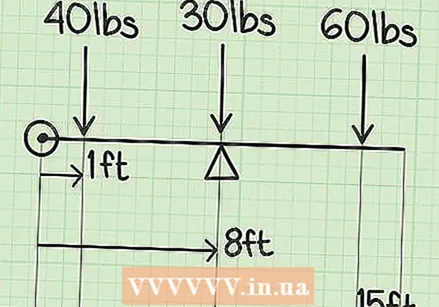2. Measure the distance from the zero point to the center of the main object as well as to the two additional weights. Let's say the children are each 1 meter from each end of the seesaw. The center of the seesaw is the center of the seesaw, or 3 meters, because 6 meters divided by 2 equals 3. Here are the distances from the center of the largest object and the two extra weights form the zero point:
   • Center of the seesaw = 4 meters from the zero point.
   • Child 1 = 1 meter from the zero point
   • Child 2 = 5 meters from the zero point

Method 3 of 4: Determine the center of gravity

1. Multiply the distance from each object to the zero point by its weight to find the moment. This gives you the moment for each object. Here's how to multiply the distance from each object to the zero point by its weight:
   • The seesaw: 30 kg x 3 m = 90 m * kg.
   • Child 1 = 40 kg x 1 m = 40 m * kg.
   • Child 2 = 60 kg x 5 m = 300 m * kg.
2. Add the three moments together. Just calculate the following: 90 m * kg + 40 m * kg + 300 m * kg = 430 m * kg. The total moment is 430 m * kg.
3. Add up the weights of all objects. Determine the sum of the weights of the seesaw and the two children. Do this as follows: 30 kilos + 40 kilos + 60 kilos = 130 kilos.
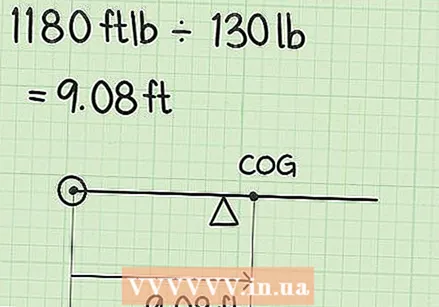4. Divide the total moment by the total weight. This will give you the distance from the zero point to the object's center of gravity. This by dividing you by 430 m * kg by 130 kilos.
   • 430 m * kg ÷ 130 kilos = 3.31 m
   • The center of gravity is 3.31 meters from the zero point, or measured from the zero point it is 3.31 meters from the end of the left side of the seesaw where the zero point was placed.

Method 4 of 4: Check your answer

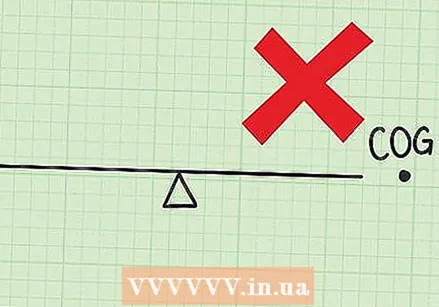1. Find the center of gravity in the diagram. If the center of gravity you have found is outside the system of objects, then you have found the wrong answer. You may have calculated the distance of more than one point. Please try again with only one zero point.
   • For example: for people sitting on the seesaw, the center of gravity must be somewhere on the seesaw, not to the left or right of the seesaw. It doesn't have to be on a person.
   • This also applies to problems in two dimensions. Draw a square just big enough to fit all the objects in your problem. The center of gravity must be within this square.
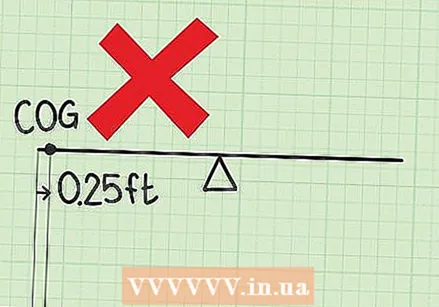2. Check your calculations if your answer is too small. If you chose one end of the system as your zero point, then a small answer places the center of gravity right next to one end. This may be the correct answer, but it is often an indication that something has gone wrong. Do you have the weight and the distance with each other in the calculation multiplied? That is the right way to find this moment. If you accidentally added together, you will probably get a much smaller answer.
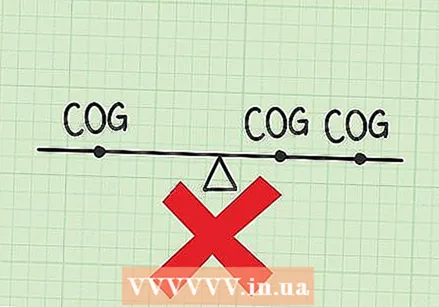3. Check your calculation if you have found more than one center of gravity. Each system has only a single center of gravity. If there are more, you may have skipped the step where you had to add all the moments together. It is the center of gravity total moment divided by the total weight. You do not have to each moment to divide by each weight, which only gives you the position of each object.
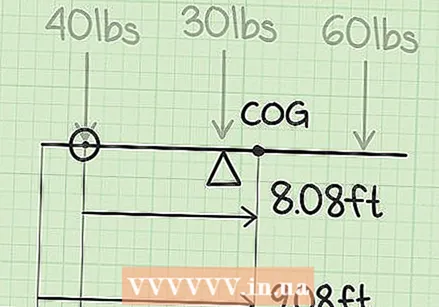4. Check the zero point if your answer is an integer next to it. The answer in our example is 3.31 m. Suppose you were given 2.31 m, 4.31 m, or some other number ending in `` .31. '' This is probably because we have the left end of the seesaw. as the zero point, while you chose the right end or another point at a distance of an integer from our zero point. Your answer is correct, regardless of the zero point you choose! You just have to remember that the zero point always stands for x = 0. Here's an example:
   • The way we solved it, the zero point is on the left side of the seesaw. Our answer is 3.31 m, so our center of mass is 3.31 m from the zero point on the left.
   • If you choose a new zero point, choose 1 m from the left, you will get 2.31 m from the center of mass as the answer. The center of mass is 2.31 m from the new zero point, or 1 m from the left. The center of mass is 2.31 + 1 = 3.31 m from the left, and with that the same answer as we had calculated above.
   • (Note: when measuring distance, remember distances left from the zero point are negative, and distances right positive.)
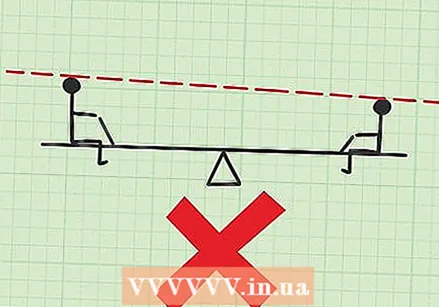5. Make sure all your measurements are straight lines. Suppose you see another example with "kids on a seesaw," but one child is much taller than the other, or a boy hangs under the seesaw instead of sitting on it. Ignore the difference and take all your measurements along the straight line of the seesaw. Measuring distances in a corner will yield answers that are close, but slightly different.
   • For seesaw exercises, all that matters is where the center of gravity is from left to right along the line of the seesaw. Later you may learn more advanced ways of calculating the center of gravity in two dimensions.

Tips

• To determine the distance over which a person has to move in order to balance the seesaw on the support, use this formula: (displaced weight) / (total weight)=(distance over which center of gravity has been moved) / (distance over which weight has been moved ). This formula can be rewritten to show that the distance the weight (person) must be moved is equal to the distance between the center of gravity and the point of support times the weight of the person divided by the total weight. So it must be the first child -1.31 m * 40 kilos / 130 kilos =-0.40 m move (to the end of the seesaw). Or should the second child turn -1.08 m * 130 kilos / 60 kilos =Move -2.84 m. (towards the center of the seesaw).
• To find the center of gravity of a two-dimensional object, use the formula Xcg = ∑xW / ∑W to find the center of gravity along the x axis, and Ycg = ∑yW / ∑W to find the center of gravity along the y axis to find. The point at which they intersect is the center of gravity.
• The definition of the center of gravity of a general mass distribution is (∫ r dW / ∫ dW) where dW is equal to the derivative of the weight, r is the position vector, and where the integrals are to be interpreted as Stieltjes integrals over the whole body. However, they can be expressed as more conventional Riemann or Lebesgue volume integrals for distributions with a probability density function. Starting with this definition, all CG properties, including those used in this article, can be derived from the Stieltjes integrals properties.

Warnings

• Don't try to blindly apply these mechanics without understanding the theory, which can lead to errors. First try to understand the underlying laws / theories.