Content

• To step
• Method 1 of 4: Determining the range of a function with a given equation
• Method 2 of 4: Determining the range of a function using a graph
• Method 3 of 4: Determining the scope of a relationship's function
• Method 4 of 4: Determine the scope of a function in an issue
• Tips

The range of a function is the set of numbers that the function can produce.In other words, it is the set of y values ​​that you get when you process all possible x values ​​in the function. This set of x values ​​is called the domain. If you want to know how to calculate the range of a function, follow the steps below.

To step

Method 1 of 4: Determining the range of a function with a given equation

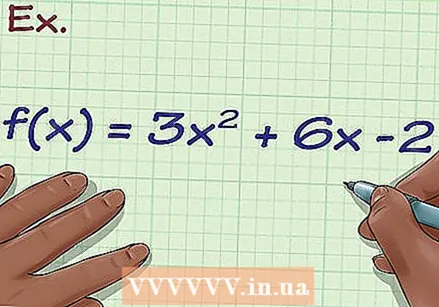1. Write down the equation. Suppose you have the following equation: f (x) = 3x + 6x -2. This means that when you enter a value for the X of the equation, you then get a yvalue. This is the function of a parabola.
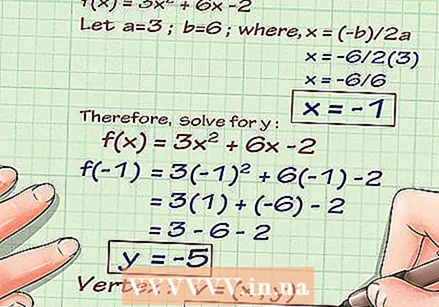2. Find the top of the function, if it is a quadratic equation. If you have a straight line or any function with a polynomial or an odd number, such as f (x) = 6x + 2x + 7, you can skip this step. But if you are dealing with a parabola or an equation where the x coordinate is squared or increases by an even power, you will have to draw the top of the parabola. Use the equation for this -b / 2a for the x coordinate of the function 3x + 6x -2, where 3 = a, 6 = b and -2 = c. In this case applies -b is -6 and 2a is 6, so the x coordinate is -6/6, or -1.
   • Then process -1 in the function to get the y coordinate. f (-1) = 3 (-1) + 6 (-1) -2 = 3 - 6 -2 = -5.
   • The top of the parabola is (-1, -5). Process this in the graph by drawing a point at x-coordinate -1 and y-coordinate -5. This should be in the third quadrant of the graph.
3. Look for a few other points of the position. To get a feel for the function, you should enter a number of other values ​​for x so that you can get an idea of ​​what the function looks like before searching for the range. Since it is a parabola and x is positive, the parabola will point upwards (valley parabola). But just to be on the safe side, we enter a number of values ​​for x to find out which y coordinates they yield:
   • f (-2) = 3 (-2) + 6 (-2) -2 = -2. One point on the graph is (-2, -2)
   • f (0) = 3 (0) + 6 (0) -2 = -2. Another point on the graph is (0, -2)
   • f (1) = 3 (1) + 6 (1) -2 = 7. A third point on the graph is (1, 7).
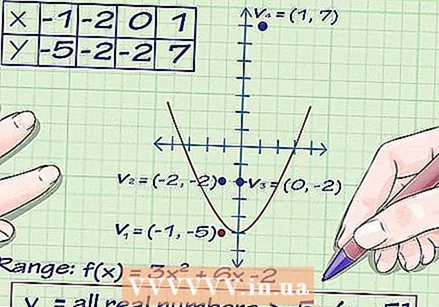4. Find the range of the chart. Now look at the y coordinates on the graph and find the lowest point where the graph touches the y coordinate. In this case, the lowest y coordinate is at the top of the parabola, -5, and the graph extends indefinitely beyond this point. This implies the scope of the function y = all real numbers ≥ -5.

Method 2 of 4: Determining the range of a function using a graph

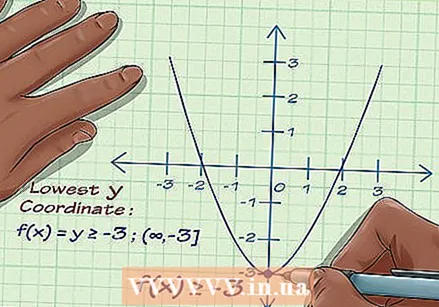1. Find the minimum of the position. Find the lowest y coordinate of the function. Suppose the function reaches its lowest point at -3. This function can get smaller and smaller, to infinity, so it has no fixed lowest point - just infinity.
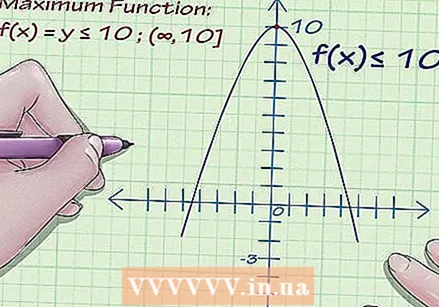2. Find the maximum of the function. Suppose the highest y-coordinate of the function is 10. This function can also become infinitely larger, so it has no fixed highest point - only infinity.
3. Indicate what the range is. This means that the range of the function, or the range of the y coordinates, is -3 to 10. So, -3 ≤ f (x) ≤ 10. That is the range of the function.
   • But suppose y = -3 is the lowest point on the graph, but it rises forever. Then the range is f (x) ≥ -3, and no more than that.
   • Suppose the graph reaches its highest point at y = 10, but then continues to fall forever. Then the range is f (x) ≤ 10.

Method 3 of 4: Determining the scope of a relationship's function

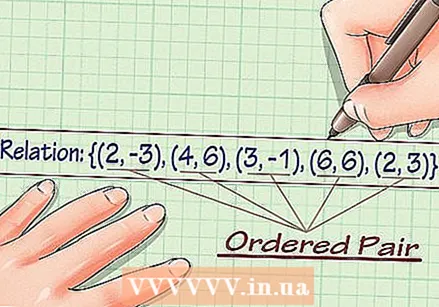1. Write down the relationship. A relationship is a collection of ordered pairs of x and y coordinates. You can look at a relationship and determine its domain and scope. Suppose you are dealing with the following relationship: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.
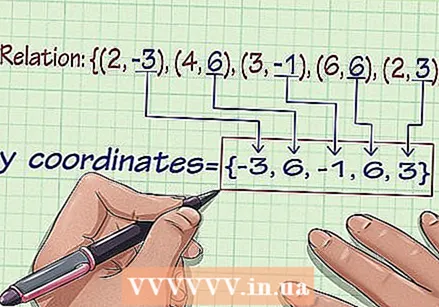2. List the y coordinates of the relationship. To determine the range of the relationship, we write down all the y coordinates of each ordered pair: {-3, 6, -1, 6, 3}.
3. Remove all duplicate coordinates so that you have only one of each y coordinate. You may have noticed that you have the "6" in the list twice. Remove it so that you are left with {-3, -1, 6, 3}.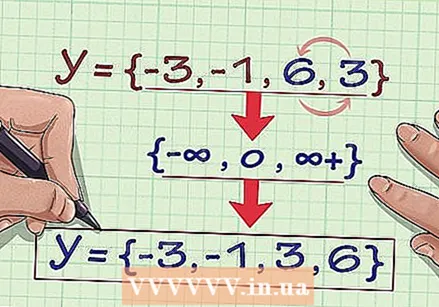
4. Write the scope of the relationship in ascending order. Then arrange the numbers in the set from smallest to largest, and you have found the range. The range of the relationship {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} is {-3, -1, 3, 6} . You are all set.
5. Make the relationship a function is. For a relationship to be a function, every time you enter a number of an x ​​coordinate, the y coordinate must be the same. For example, the relationship is {(2, 3) (2, 4) (6, 9)} no function, because if you enter 2 as x for the first time, you get 3 as value, but the second time you enter 2, you get four. A relationship is only a function if you always get the same output for a certain input. If you enter -7, you should get the same y coordinate (whatever that may be) every time.

Method 4 of 4: Determine the scope of a function in an issue

1. Read the issue. Suppose you are working on the following assignment: "Becky sells tickets to her school's talent show for $ 5 each. The total amount she raises is a function of the number of tickets she sells. What is the scope of the feature?"
2. Write the problem as a function. In this case M. the amount raised and t the number of tickets sold. Since each ticket costs 5 euros, you will have to multiply the number of tickets sold by 5 to get the total amount. Therefore, the function can be written as M (t) = 5t.
   • For example: If she sells 2 tickets, you will have to multiply 2 by 5, to answer 10, and thus the total amount raised.
3. Determine what the domain is. To find the range you first need the domain. The domain consists of all possible values ​​of t that participate in the equation. In this case, Becky can sell 0 or more tickets - she cannot sell a negative number of tickets. Since we do not know the number of seats in the school's auditorium, we can assume that in theory it can sell an infinite number of tickets. And she can only sell whole cards, not part of them. Hence, it is the domain of the function t = any positive integer.
4. Determine the range. The range is the possible amount that Becky can raise with the sale. You will have to work with the domain to find the range. If you know that the domain is a positive integer and that the equation M (t) = 5t then you also know that you can enter any positive integer in this function for the answer, or range. For example: If she sells 5 tickets, then M (5) = 5 x 5, or $ 25. If she sells 100, then M (100) = 5 x 100, or 500 euros. Hence, the scope of the function any positive integer that is a multiple of five.
   • That is, any positive integer that is a multiple of five is a possible outcome of the function.

Tips

• See if you can find the inverse of the function. The domain of the inverse of a function is equal to the range of that function.
• In more difficult cases, it may be easier to first draw the graph using the domain (if necessary) and then read the range from the graph.
• Check if the function repeats. Any function that repeats along the x axis will have the same range for the entire function. For example: f (x) = sin (x) has a range between -1 and 1.