Content

• Warnings
• Tips

An arithmetic sequence is any sequence of numbers that, in sequence, differ from each other by a constant value. For example, the sequence of even numbers, ${ displaystyle 0.2,4,6,8}$Find the difference factor of the series. When you are presented with a set of numbers, it may be stated that it is an arithmetic sequence, or you may have to figure this out yourself. The first step is in any case the same. Select the first two consecutive numbers in the collection. Subtract the first number from the second number. The result is the difference factor of your sequence.

• For example, suppose you have the collection ${ displaystyle 1,4,7,10,13}$Check that the difference factor is constant. Determining the difference factor for only the first two numbers does not ensure that the set is an arithmetic sequence. You have to be sure that the difference is consistently maintained throughout the sequence. Check the difference by subtracting two consecutive numbers in the set. If the result is consistent for one or two other pairs of numbers, you are probably dealing with an arithmetic sequence.
  • We continue to work with the same example, ${ displaystyle 1,4,7,10,13}$Add the difference factor to the last number. It is easy to find the next number in an arithmetic sequence when you know the difference factor. Just add the difference factor to the last last number of the set and you get the next number.
    • For example, in the example of ${ displaystyle 1,4,7,10,13}$Confirm that you are starting with an arithmetic sequence. In some cases you are dealing with a set of numbers with a missing number in the middle. As mentioned earlier, start by checking that your collection is an arithmetic sequence. Select two consecutive numbers and find the difference between them. Then check this against two other consecutive numbers in the sequence. If the difference is the same, you can assume that you are dealing with an arithmetic sequence and you can continue.
      • For example, suppose you have the sequence ${ displaystyle 0.4}$Add the difference factor to the number for the empty space. This is equivalent to adding a number to the end of a sequence. Find the number immediately before the empty spot in your sequence. This is the "last" number known. Add the difference found to this number, and you get the number that should fit the place of the unknown.
        • In our example, ${ displaystyle 0.4}$Subtract the difference factor from the number after the unknown. To make sure you have found the correct answer, check again from the other direction. An arithmetic sequence should be consistent in one direction. If you go from left to right and keep adding 4, you can do the opposite from right to left and subtract 4 from the previous number.
          • In the example, ${ displaystyle 0.4}$Compare your outcomes. The two results you get from addition (left to right) or subtraction (right to left) should match. If so, you have found the missing number. If they don't match, you should check your work again. You may not be dealing with a pure arithmetic sequence.
            • In the example, the two outcomes of ${ displaystyle 4 + 4}$Find the first number of the series. Not every sequence starts with the numbers 0 or 1. Look at the set of numbers you have and determine the first number. This is your starting point, which can be indicated with variables, such as a (1).
              • It is common practice to work with arithmetic sequences with the variable a (1), which indicates the first number in the sequence. You can of course choose any variable, but the outcome should be the same.
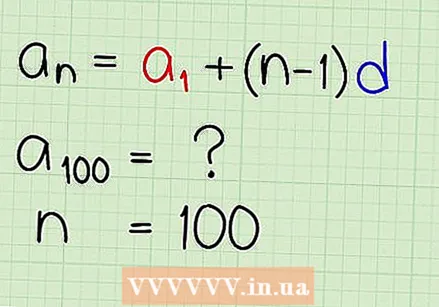              • For example, given the series ${ displaystyle 3,8,13,18}$Determine the difference factor as d. Determine the difference factor for the series as indicated above. In this example, the difference factor is equal to ${ displaystyle 8-3}$Use the explicit formula. An explicit formula is a math equation you can use to find any number in an arithmetic sequence without having to write out the entire sequence. The explicit formula for a mathematical sequence is ${ displaystyle a (n) = a (1) + (n-1) d}$Fill in all the information to solve the problem. Using this explicit formula for your sequence, fill in all the data you have to determine the number you need.
                • For example, in this example, 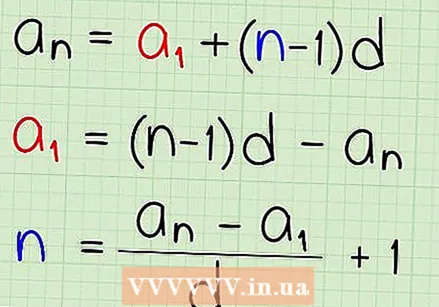${ displaystyle 3,8,13,18}$Rearrange the explicit formula to find other variables. Use the explicit formula and some simple algebra to find various bits of information about the arithmetic sequence. In its original form (${ displaystyle a (n) = a (1) + (n-1) d}$Find the first number of a series. You may know that the 50th number in an arithmetic sequence equals 300 and the numbers increase by 7 (the difference factor), but you would like to know what the first number in the sequence was. Use the modified explicit formula for solving a1 to find out your answer.
                  • Use the equation ${ displaystyle a (1) = (n-1) d-a (n)}$Determine the length of a sequence. Suppose you know how the sequence begins and ends, but you need to find out how long the sequence is. Then use the modified formula ${ displaystyle n = { frac {a (n) -a (1)} {d}} + 1}$.
                    • Suppose you know that a given arithmetic sequence starts with 100 and adds up with 13. It is also given that the last number is 2856. To find the length of the sequence, use the numbers a1 = 100, d = 13, and a (n) = 2856. Apply these numbers to the formula for getting ${ displaystyle n = { frac {2856-100} {13}} + 1}$. Once you have worked this out, you will get ${ displaystyle n = { frac {2756} {13}} + 1}$, which is equal to 212 + 1, which is again 213. There are 213 numbers in that sequence.
                    • This example looks like 100, 113, 126, 139… 2843, 2856.

                  Warnings

                  • There are different types of series of numbers. Do not assume that a set of numbers is an arithmetic sequence. Always check two pairs of numbers, preferably three or four, to find the difference factor for the series of numbers.

                  Tips

                  • Do not forget that d can be either positive or negative, depending on whether there is an addition or a subtraction.