Content

• Steps
• Advice
• Warning

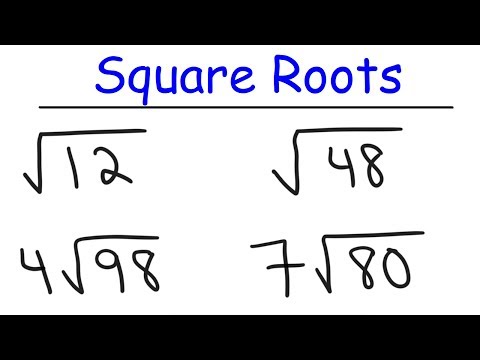
Simplifying the square root is not difficult, we just need to separate the lower root into factors, where at least one factor is the square root, and then draw out the square root sign of the main number. that way. Once you have memorized some common perfect squares and know how to factor numbers, reducing your square root is "as easy as eating a candy".

Steps

Method 1 of 3: Simplify the square root by factor analysis

1. 

   Understand what factor analysis is. The goal of reducing the square root is to rewrite it in a simpler and easier way to solve math problems. Factor analysis is a way of dividing a larger number into many factor smaller than, for example, splitting 9 into 3 x 3. Once we have found the factors of the number in question, we can rewrite the square root of that number into a simpler form, maybe even an integer. . For example, √9 = √ (3x3) = 3. The steps below will show you the more complicated process of reducing square roots.

2. 

   
   
   Divide the lower number by the smallest prime number possible. If the bottom part is even, divide by two. If it's an odd number then try to see if it is divisible by 3. In the case the lower-radical number is not divisible by both 2 and 3, proceed with the next prime number in the list below until you find the smallest prime divisor of the number below the root. We only consider primes because all other numbers can analyze the performance of some primes with other factors. For example, we wouldn't divide the base by 4, because any number divided by 4 would be divisible by 2.
   • 2
   • 3
   • 5
   • 7
   • 11
   • 13
   • 17

3. 

   
   
   Rewrite the square root in the form of the multiplication problem. Keep all factors under radical signs. For example, when we simplify √98, we see 98 ÷ 2 = 49, so 98 = 2 x 49. So we could rewrite it as: √98 = √ (2 x 49).

4. 

   Repeat the above steps for the remaining factor. Before reducing the square root we are considering, we need to divide the factor until we have the results of the analysis that two numbers are identical. Recalling what it means to be a square root, it makes perfect sense: because √ (2 x 2) means "a number that, when multiplied by itself, will give you 2 x 2." And clearly in this case it is the number 2. Similarly, we repeat these steps with the example we consider √ (2 x 49):
   • We have separated factor 2. (In other words, this is one of the prime numbers listed above). So, we'll ignore this number and continue to split 49 into smaller factors.
   • 49 is not divisible by 2, 3, or 5. We can verify it by using a calculator or doing division. Since the result of division 49 by 2, 3 or 5 doesn't give us an integer, we will ignore these numbers and divide it up.
   • 49 may divisible by 7. We have 49 ÷ 7 = 7, that is, 49 = 7 x 7.
   • To rewrite the problem, we get: √ (2 x 49) = √ (2 x 7 x 7).

5. 

   
   
   "Pull" a number from the root sign. Once we have broken the number into factors in which two numbers are identical, we can pull that number out of the radical sign. All remaining factors remain under the radical sign. For example: √ (2 x 7 x 7) = √ (2) √ (7 x 7) = √ (2) x 7 = 7√ (2).
   • We can stop the analysis once two similar factors have been found. For example √ (16) = √ (4 x 4) = 4. If we continue with the analysis, the final result will not change, the only difference is that we have to do the division more times: √ (16) = √ (4 x 4) = √ (2 x 2 x 2 x 2) = √ (2 x 2) √ (2 x 2) = 2 x 2 = 4.

6. 

   If the number of underlying factors is more than one, then we multiply them. With large square roots, you can perform the reduction many times. In that case, the factor product will yield the final result. Consider the following example:
   • √180 = √ (2 x 90)
   • √180 = √ (2 x 2 x 45)
   • √180 = 2√45, but the remaining radical can still be further analyzed into a smaller factor
   • √180 = 2√ (3 x 15)
   • √180 = 2√ (3 x 3 x 5)
   • √180 = (2)(3√5)
   • √180 = 6√5

7. 

   Record "cannot be reduced" if factor analysis does not give two numbers the same. Some of the square roots are already in the simplified form. If we continue to analyze until all the underlying factors are prime (mentioned in the steps above) and no two numbers are the same, then we cannot further reduce it. Maybe the topic in question is just a tip! For example, let's simplify √70:
   • 70 = 35 x 2, so √70 = √ (35 x 2)
   • 35 = 7 x 5, so √ (35 x 2) = √ (7 x 5 x 2)
   • All three numbers above are prime, so we cannot reduce it any further. In addition, these three numbers are different, so it is not possible to pull one of the three numbers out of the radical. So √70 cannot be shortened anymore.
   advertisement

Method 2 of 3: The perfect square

1. 

   Memorize the square numbers. Squaring a number, in other words multiplying a number by itself, gives a perfect square result. For example, 25 is a perfect square because 5 x 5, which is 5, equals 25. Try to memorize at least the first ten perfect squares because they can help you easily recognize the corresponding square root. The first ten perfect squares are:
   • 1 = 1
   • 2 = 4
   • 3 = 9
   • 4 = 16
   • 5 = 25
   • 6 = 36
   • 7 = 49
   • 8 = 64
   • 9 = 81
   • 10 = 100
   • Find the square root of a perfect square number. If we see a perfect square under the radical sign, we can convert it to the product of two identical numbers, thereby eliminating the radical sign. For example, when we see that the lower root is 25, we know that the value of this square root is 5 because 25 is a perfect square and is 5 x 5. Similarly, we have the square root of the square root. the above is as follows:

     

   • √1 = 1
   • √4 = 2
   • √9 = 3
   • √16 = 4
   • √25 = 5
   • √36 = 6
   • √49 = 7
   • √64 = 8
   • √81 = 9
   • √100 = 10

2. 

   Analyze the factors into perfect squares. When reducing the square root, use the square numbers in the factor analysis step. If you can split a perfect square, reducing it will take less time. Here are some tips:
   • √50 = √ (25 x 2) = 5√2. If the last two digits of the number being considered are 25, 50 or 75, we always separate the number 25 from that number.
   • √1700 = √ (100 x 17) = 10√17. If the last two digits of the number in question are 00, 100 is always separated from that number.
   • √72 = √ (9 x 8) = 3√8. Knowing the multiples of 9 also helps a lot when it comes to factor analysis. The trick to realize multiples of 9 is as follows: if the sum all the digits of the number being considered are 9 or divisible by 9, the number is divisible by 9.
   • √12 = √ (4 x 3) = 2√3. There is no trick to tell if a number is divisible by 4, but for numbers that are not too large, doing the division by 4 isn't too complicated. Keep this in mind when analyzing the factor.

3. 

   Analyze some accomplishments of many perfect squares. If the number in question is the product of more than a perfect square, we can put everything outside the radical sign. In the process of reducing the square root, if the factor analysis results have many perfect squares, we withdraw their square roots from the radical sign and multiply it together. For example, √72:
   • √72 = √ (9 x 8)
   • √72 = √ (9 x 4 x 2)
   • √72 = √ (9) x √ (4) x √ (2)
   • √72 = 3 x 2 x √2
   • √72 = 6√2
   advertisement

Method 3 of 3: Glossary

1. 

   The sign (√) is the square root sign. For the example in the √25 problem, "√" is the root sign.

2. 

   The number under the radical is the number written under the radical sign. We need to find the square root of that number. For example, where √25, "25" is the number under the root.

3. 

   The radical coefficient is the number outside the radical sign. This is the multiplier of the square root and to the left of the square root. For 7√2, for example, "7" is the coefficient.

4. 

   The result of a division is called a factor. For example, 2 is a factor of 8 because 8 ÷ 4 = 2, 3 is not a factor of 8 because 8 ÷ 3 does not return an integer. For example, 5 is a factor of 25 because 5 x 5 = 25.

5. 

   The meaning of reducing the square root. Reducing a square root is separating the square root of the number below the root, extracting the square root of those squared numbers from the radical sign, while keeping the remaining factor under the radical sign. If the number under the root is a perfect square, then after reduction we will eliminate the radical sign. For example, √98 can be reduced to 7√2. advertisement

Advice

• One way to divide a perfect square into a factor is to go through the list of perfect squares, start trying from the number that is closest to the bottom radical number, and stop when you find a number that is a divisor of the number below the root. .For example, when you find a perfect square that can be extracted from 27, you would start at 25 then 16 and stop at 9 because this is a divisor of 27.
• We need to find a number that, when multiplied by itself, will result in a number under the radical sign. For example, the square root of 25 is 5 because if we take 5 x 5 we get 25. It's as easy as eating candy!

Warning

• The calculator is quite useful when you need to deal with large numbers, but the more you try to practice this type of exercise yourself, the easier it will be to reduce the square root for you.
• Simplify and estimate values ​​are not the same. The process of reducing the square root cannot result in a decimal number.