Content

• To step
• Method 1 of 2: The length of the sides of a right triangle
• Method 2 of 2: Calculate the distance between two points in the plane
• Tips

The Pythagorean Theorem describes the length of the sides of a right triangle in a way so elegant and practical that it is still widely used today. This states that for any right triangle, the sum of the squares of straight sides is equal to the square of the hypotenuse. In other words, for a right triangle (a triangle with sides perpendicular to each other), with sides of length a and b and a hypotenuse of length c: a + b = c. The Pythagorean theorem is one of the pillars of geometry and has numerous practical applications - using this theorem, for example, it is very easy to find the distance between two points in a flat plane.

To step

Method 1 of 2: The length of the sides of a right triangle

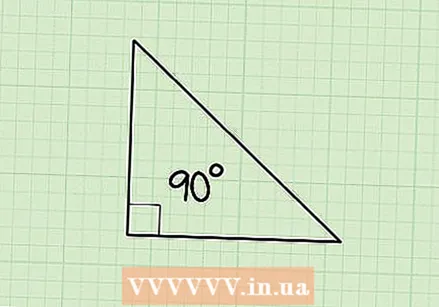1. Check if you are dealing with a right triangle. The Pythagorean theorem can only be used with right triangles, so before proceeding it is important to verify that your triangle meets the definition of a right triangle. Fortunately, there is only one factor that is decisive in this regard - one of the angles of the triangle must be a 90 degree angle.
   • As a clue, right angles are often marked with a small square bracket to indicate that this is a 90 degree angle. Check if there is such a parenthesis in one of the corners of your triangle.
2. Assign the variables a, b, and c to the sides of your triangle. In the Pythagorean theorem, the variables a and b refer to the right sides of your triangle, and the variable c to the hypotenuse - the long side opposite the right angle. So to begin with, you assign variables a and b (the order does not matter) to the straight sides and c you assign to the hypotenuse.
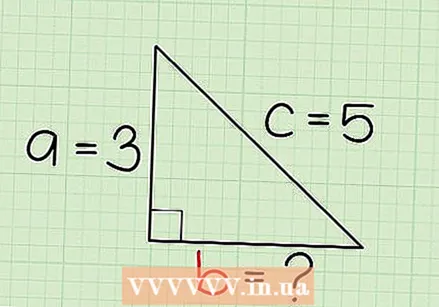3. Determine which side of the triangle you want to know. The Pythagorean Theorem allows you to find the length of each side of a triangle, provided two of the sides are known. Determine which of the sides has an unknown length - a, b, and / or c. If only one is unknown, you can proceed.
   • Suppose we know that the hypotenuse has a length of 5 and one of the other sides has a length of 3. The length of the remaining side is unknown. Since two of the sides are known, we can proceed to calculate the length of the unknown side! We will use this example again later.
   • If the length of two of the sides are unknown, you must determine the length of at least one more side to be able to use the Pythagorean theorem. The basic trigonometric functions can help you with this, provided you know one of the other, non-right angles of the triangle.
4. Calculate using the equation and the people you know. Enter the values ​​for the length of the sides of your triangle into the equation a + b = c. Remember that a and b are the straight sides and c is the hypotenuse.
   • In our example, we know the length of one side and that of the hypotenuse (3 & 5), so we write our equation like this: 3² + b² = 5²
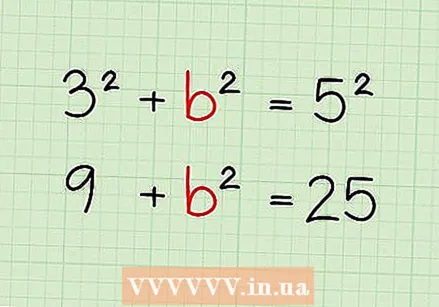5. Calculate the squares. To solve your equation, start by squaring each of the known sides. If you find this easier, you can leave the power and only square it later.
   • In our example, we square 3 and 5 to get resp. 9 and 25 to get. We can now rewrite the equation as 9 + b² = 25.
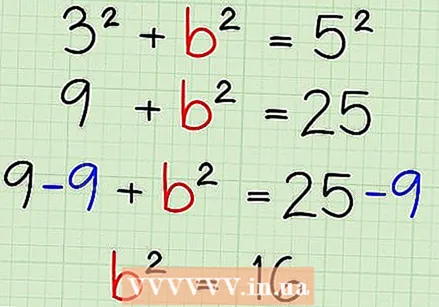6. Isolate the unknown variable on one side of the equal sign. If necessary, use standard algebraic operations to get the unknown to one side of the equals sign and squares to the other. If you're trying to find the hypotenuse, then c in the theorem is already on one side, so you can skip that step.
   • In our example, the equation is now 9 + b² = 25. To isolate b & sup2, we subtract 9 from both sides of the equation. This leaves us with b² = 16.
7. Take the square root of both sides of the equation. You should now have a square (variable) on one side of the equation and a number on the other. Now pull the square root of both sides to find the length of the unknown.
   • In our example, b² = 16, the equation after square rooting is b = 4. So we can say that the length of the unknown side of our triangle is equal to 4.
8. Use the Pythagorean theorem in practice. The reason the Pythagorean theorem is used so much is because it is applicable for solving many practical problems. Learn to recognize right triangles in the world around you - wherever you can recognize a right triangle on one or more objects, the Pythagorean theorem is applicable to find the length of one of the sides, provided there are two sides or angles. be famous.
   • Let's take an example from the real world. A ladder is leaning against a wall. The bottom of the ladder is 5 meters away from the wall. The ladder reaches 20 meters from the bottom of the wall. How long is the ladder?
     • "5 meters is the distance to the wall" and "the ladder is 20 meters high". This gives an indication of the length of the sides of the triangle. Since we may assume that the wall and the ground form a right angle and the ladder is diagonally against the wall at an angle, we can consider this arrangement as a right triangle, the sides of which have a length of a = 5 and b = 20. The length of the ladder is the hypotenuse, the unknown variable c. Let's apply the Pythagorean theorem:
       • a² + b² = c²
       • (5) ² + (20) ² = c²
       • 25 + 400 = c²
       • 425 = c²
       • sqrt (425) = c
       • c = 20.6. The length of the ladder is (approximate) 20.6 meters.

Method 2 of 2: Calculate the distance between two points in the plane

1. Define two points in the plane. The Pythagorean theorem can be used very easily to find the straight-line distance between two points in the plane. All you need is the x and y coordinates of any two points. Usually these coordinates are written as (x, y).
   • To find the distance between these two points, we consider each of the points as one of the vertices of a right triangle, which does not belong to the right angle. This makes it very easy to find the length of a and b, after which c (the hypotenuse and the distance between the two points) can be calculated.
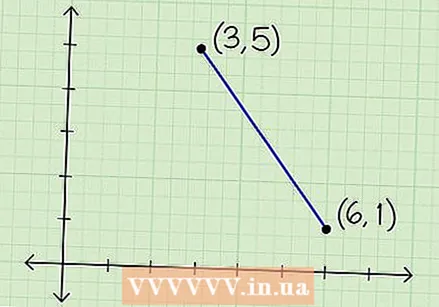2. Draw the two points on a graph. In an X-Y plane, for each point (x, y), x is a point on the horizontal x-axis and y is a point on the vertical y-axis. You can find the distance between the two without graphing them, but doing so will give you a visual reference that you can use to check if your answer makes sense.
3. Determine the length of the straight sides of your triangle. By considering your two points as the angles of the triangle adjacent to the hypotenuse, you can find the length of sides a and b. You can do this by using the graph, or by using the formulas | x₁ - x₂| for the horizontal side and | y₁ - y₂| for the vertical side, where (x₁, y₁) is the first point and (x₂, y₂) the second point.
   • Suppose we have points (6,1) and (3,5). The length of the horizontal side of our triangle is:
     • | x₁ - x₂|
     • |3 - 6|
     • | -3 | = 3
   • The length of the vertical side is:
     • | y₁ - y₂|
     • |1 - 5|
     • | -4 | = 4
   • So we can say that the length of the sides of our right triangle is equal to a = 3 and b = 4.
4. Use the Pythagorean theorem to find the hypotenuse. The distance between the two points is the length of the triangle's hypotenuse. Use the Pythagorean Theorem to find the hypotenuse of the triangle, with sides a, b, and c.
   • In our example, we know the points (3,5) and (6,1), and the lengths of the sides are a = 3 and b = 4, so we determine the hypotenuse as follows:

     • (3) ² + (4) ² = c²

       c = sqrt (9 + 16)

       c = sqrt (25)

       c = 5. The distance between (3,5) and (6,1) is 5.

Tips

• If the triangle is not a right triangle, then you cannot just use the Pythagorean theorem.
• The hypotenuse is always:
  • the line opposite the right angle
  • the longest side of the right triangle
  • the variable c in the Pythagorean theorem
• sqrt (x) means "the square root of x".
• Don't forget to always check your answers. If an answer appears to be incorrect, check your calculations or start over.
• If you only know one side of the triangle, but also one of the other angles (then the right angle), first calculate another side with what you know about trigonometry (sin, cos, tan) or the proportions 30-60- 90 / 45-45-90.
• Another check - the longest side is opposite the greatest angle and the shortest side is opposite the smallest angle.