Content

• To step
• Method 1 of 1: Part Two: Using the sum of 1 to N to find the sum of two integers
• Tips
• Warnings

Integers are integers without fractions or decimals. If a math problem requires you to calculate the sum of a number of integers from 1 to a given value N, then it is not necessary to add each value by hand. Instead, to save time and effort, use the equation (N (N + 1)) / 2, where N is the highest number in the series.

To step

1. Define the largest integer as N. When adding integers from 1 to a given number N., you must define N itself as a positive integer. N is an integer, so it cannot be a decimal number or fraction. N must also not be negative.
   • As an example, let's say we want to add all integers from 1 to 100. In this case, 100 is the value for N because it is the last number in our series, or, in other words, the largest number in the addition.
2. Multiply N (N + 1) and divide by 2. When you have defined the value of N, apply this value to the equation (N (N + 1)) / 2. This equation finds the sum of all integers between 1 and N.
   • In our example, we enter 100, the value for N, into the equation. (N (N + 1)) / 2 then becomes (100 (100 + 1)) / 2.
3. Calculate the answer. The final value of this equation is the sum of all numbers between 1 and N.
   • Let's solve this example.
     • (100(100 + 1))/2 =
     • (100(101))/2 =
     • (10100)/2 =
     • 5050. Is the sum of all integers from 1 to 100 5050.
4. Understand how the equation (N (N + 1)) / 2 is derived. Take another look at the sample problem. Divide this sequence 1 + 2 + 3 + 4 ... + 99 + 100 into two groups - from 1 to 50 and one from 51 to 100. If you add the first number in the first group (1) to the last number in the second group (100), you get 101. You get the same answer (101) with 2 + 99, 3 + 98, 4 + 97, and so on. If we add each number in the first group to the corresponding number in the second group, we end up with 50 pairs of numbers with the same sum: 101. So, 50 x 101 = 5050, the sum for the integers from 1 to 100. Note that 50 is half of 100, and 101 is 100 + 1. In fact, this observation holds for the sum of any positive integer - the addition of the components can be divided into two groups, and the numbers in these groups can be assigned to each other in such a way that each pair has the same sum. Note that for an odd sequence of integers, one number remains - this does not affect the final answer.
   • In general, we can say that for any number N, the sum of the numbers from 1 to N is equal to (N / 2) (N + 1). The simplified form of this equation is (N (N + 1)) / 2, which is the sum of integers equation.

Method 1 of 1: Part Two: Using the sum of 1 to N to find the sum of two integers

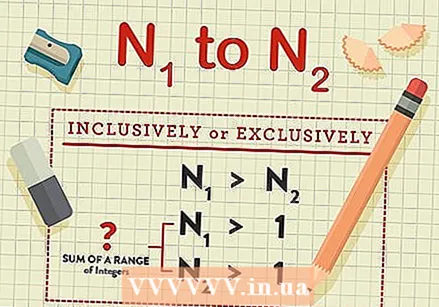1. Decide whether you add inclusive or exclusive. Often times the goal is not to sum a range of integers from 1 to a given number, but you will be asked to find the sum of a range of integers between two integers N.₁ and N₂, where N₁ > N₂ and both are> 1. The process for finding this sum is relatively simple, but before we get started, we need to decide whether the sum is inclusive or exclusive - in other words, whether the N₁ and N₂ includes or only the integers in between, because the procedure differs slightly from each other in these cases.
2. For determining the sum of the integers between two numbers N.₁ and N₂ we first determine the sum of each value of N separately and subtract it. In general, you just need to subtract the sum of the smaller N value from the sum of the larger N value to find the answer. However, as indicated above, it is important to know whether this addition is inclusive or exclusive. Including addition requires you to subtract 1 from the value of N.₂ before entering it into the equation, while exclusive enumeration requires you to subtract 1 from the value for N.₁.
   • Let's say the inclusive sum of the integers between N.₁ = 100 and N₂ = 75. In other words, we have to find the sum of the series 75 + 76 + 77 ... + 99 + 100. To do this, we take the sum of the integers from 1 to N₁, and subtract that sum from the integers from 1 to N.₂ - 1 (remember that we add inclusive, so subtract 1 from N.₂), and work it out like this:
     • (N₁(N₁ + 1)) / 2 - ((N₂-1) ((N₂-1) + 1))/2 =
     • (100(100 + 1))/2 - (74(74 + 1))/2 =
     • 5050 - (74(75))/2 =
     • 5050 - 5550/2 =
     • 5050 - 2775 = 2275. The inclusive sum of the integers between 75 and 100 is 2275.
   • Now let's exclusive start counting. The equation remains the same, except that we subtract 1 from N in this case₁ instead of N.₂:
     • ((N₁-1) ((N₁-1) + 1)) / 2 - (N₂(N₂ + 1))/2 =
     • (99(99 +1))/2 - (75(75 + 1))/2 =
     • (99(100))/2 - (75(76))/2 =
     • 9900/2 – 5700/2 =
     • 4950 - 2850 = 2100. The exclusive sum of the integers between 75 and 100 is 2100.
3. Understand why this process works. Consider the sum of the integers from 1 to 100 as 1 + 2 + 3 ... + 98 + 99 + 100 and the sum of the integers from 1 to 75 as 1 + 2 + 3 ... + 73 + 74 + 75. The inclusive sum of the integers from 75 to 100 means 75 + 76 + 77 ... + 99 + 100. The sum of 1-75 and 1-100 are the same up to 75 -– at that point the sum of 1-75 'stops' and the sum of 1 - 100 continues, with ... 75 + 76 + 77 ... + 99 + 100. Therefore, subtracting the sum of the integers from 1-75 from the sum of the integers from 1-100 us the ability to separate the sum of the integers from 75-100.
   • However, if we add inclusive, we must use the sum of 1-74 instead of the sum of 1-75 to make sure that 75 is included in the final sum.
   • Likewise, when adding exclusively, we use the sum of 1-99, instead of the sum of 1-100, to make sure that 100 is not included in the sum. We can use the sum of 1-75 because subtracting this sum from the sum of 1-99 excludes the number 75 from our final sum.

Tips

• The result is always an integer, because n or n + 1 is even and can therefore be divided by 2.
• In short: SUM (1 to n) = n (n + 1) / 2
• SUM (a to b) = SUM (1 to b) - SUM (1 to a-1).
  
  

Warnings

• While generalizations to negative numbers are not very difficult, this explanation is limited to all positive integers N, where N is at least 1.