Determine the correlation coefficient

Content

To step
Method 1 of 4: Calculate the correlation coefficient by hand
Method 2 of 4: Using online correlation calculators
Method 3 of 4: Using a graphing calculator
Tips
Warnings

The correlation coefficient, denoted r or ρ, is the measure of the linear correlation (the relationship, both in strength and direction) between two variables. It ranges from -1 to +1, using plus and minus signs to represent the positive and negative correlation. If the correlation coefficient is exactly -1, then the relationship between the two variables is completely negative; if the correlation coefficient is exactly +1, then the relationship is completely positive. Two variables can have a positive correlation, a negative correlation, or no correlation at all. You can calculate the correlation by hand, using some of the free correlation calculations available online, or by using the statistical functions of a good graphing calculator.

To step

Method 1 of 4: Calculate the correlation coefficient by hand

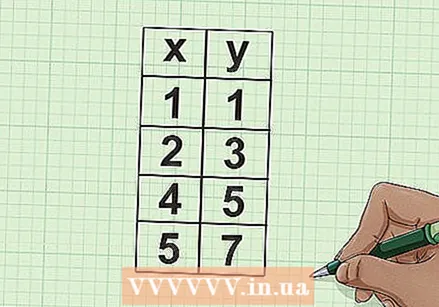First collect your data. To start calculating an efficient correlation, first examine the data pairs. It is useful to put them in a table, both vertically and horizontally. Label each row or column x and y.
- For example, suppose you have four data pairs for X and y. The table may then look like this:
  - x || y
  - 1 || 1
  - 2 || 3
  - 4 || 5
  - 5 || 7
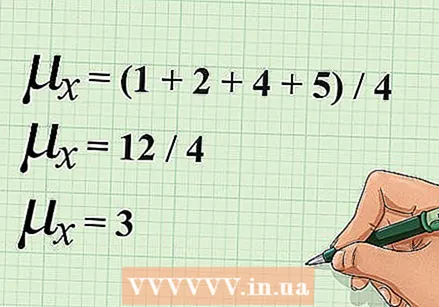Calculate the mean of X. To calculate the mean, you need all values of X add and then divide by the number of values.
- Using the example above, notice that you have four values for X. To calculate the mean, you add up all the values X and divide it by 4. The calculation looks like this:
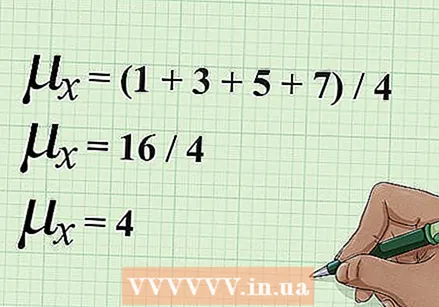- μX=(1+2+4+5)/4{ displaystyle mu _ {x} = (1 + 2 + 4 + 5) / 4}Determine the mean of y. To the average of y To find it, follow the same steps, adding all the values of y together and then dividing by the number of values.
  - In the example above, you also have four values for y. Add all these values together and then divide them by 4. The calculations will look like this:
  - μy=(1+3+5+7)/4{ displaystyle mu _ {y} = (1 + 3 + 5 + 7) / 4}Determine the standard deviation of X. Once you have your means, you can calculate the standard deviation. To do this, use the formula:
    - σX=1n−1Σ(X−μX)2{ displaystyle sigma _ {x} = { sqrt {{ frac {1} {n-1}} Sigma (x- mu _ {x}) ^ {2}}}}Calculate the standard deviation of y. Using the same basic steps, find the standard deviation of y. You're going to use the same formula, using the data points for y.
      - With the sample data, your calculations will look like this:
      - ${ displaystyle sigma _ {y} = { sqrt {{ frac {1} {4-1}} * ((1-4) ^ {2} + (3-4) ^ {2} + ( 5-4) ^ {2} + (7-4) ^ {2})}}}$ Review the basic formula for determining a correlation coefficient. The formula for calculating a correlation coefficient uses means, standard deviations, and the number of pairs in a data set (represented by n). The correlation coefficient itself is represented by the lowercase letter r or the Greek letter ρ (rho). For this article, we will use the formula known as the Pearson correlation coefficient as shown below:
        ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } right) * left ({ frac {y- mu _ {y}} { sigma _ {y}}} right)}$ Determine the correlation coefficient. You now have the means and standard deviations for your variables, so you can move on to the correlation coefficient formula. Remember that n represents the number of values you have. You have already worked out the other relevant information in the steps above.
        Using the sample data, you could enter the data into the correlation coefficient formula and calculate it as follows:
        ${ displaystyle rho = left ({ frac {1} {n-1}} right) Sigma left ({ frac {x- mu _ {x}} { sigma _ {x}} } right) * left ({ frac {y- mu _ {y}} { sigma _ {y}}} right)}$ Interpret the result. For this data set, the correlation coefficient is 0.988. This number tells you two things about the data. Look at the sign of the number and the size of the number.
        Since the correlation coefficient is positive, you can say that there is a positive correlation between the x data and the y data. This means that if the x values increase, you expect the y values to increase as well.
        Since the correlation coefficient is very close to +1, the x data and y data are very closely related. If you were to graph these points, you would see that they are a very good approximation to a straight line.

Method 2 of 4: Using online correlation calculators

Search online for correlation calculators. Measuring correlation is a fairly standard calculation for statisticians. The calculation can become very tedious for large data sets if done by hand. Therefore, many sources have made common correlation calculations available online. Use any search engine and enter the search term "correlation calculator".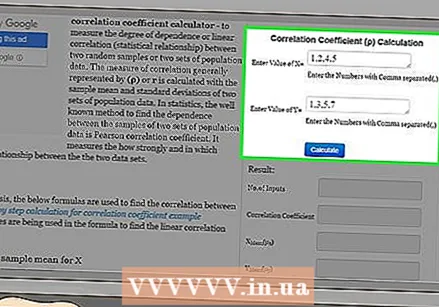
Enter the data. Read the instructions on the website carefully so that you can enter the data correctly. It is important that data pairs are kept in order or you will get an incorrect correlation result. Different websites use different formats to enter data.
- For example, on the website http://ncalculators.com/statistics/correlation-coefficient-calculator.htm you will find a horizontal box for inputting x values and a second horizontal box for inputting y values. You enter the terms, separated only by commas. Thus, the x data set calculated earlier in this article should be entered as 1,2,4,5. The y data set is entered as 1,3,5,7.
- At another site, http://www.alcula.com/calculators/statistics/correlation-coefficient/, you can enter data horizontally or vertically, as long as you keep the data points in order.
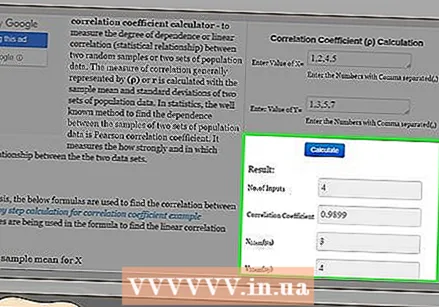Calculate the results. These calculation sites are popular because after entering the data you generally only need to click the "Calculate" button - the result will appear automatically.

Method 3 of 4: Using a graphing calculator

Enter your details. On your graphing calculator, enable the statistics function and then select the command "Edit".
- Each calculator has slightly different key commands. This article provides the specific instructions for the Texas Instruments TI-86.
- To access the Stat function, press [2nd] -Stat (above the "+" key) and then press F2-Edit.
Delete all old stored data. Most calculators will keep the statistical data until it is cleared. To make sure you don't confuse old data with new data, you should first erase all previously saved information.
- Use the arrow keys to move the cursor to highlight the "xStat" category. Then press "Clear" and "Enter. This should clear all values in the xStat column.
- Use the arrow keys to highlight the "yStat" category. Press "Clear" and "Enter" to also clear the data for that column.
Enter your data values. Use the arrow keys to move the cursor to the first space below the xStat header. Type in your first data value and then press Enter. You should see the space at the bottom of the screen "xStat (1) = __", where your value fills the empty space. When you press Enter, the data will fill the table, the cursor will move to the next line, and the line at the bottom of the screen should now read "xStat (2) = __".
- Continue entering all x values.
- When you have entered the x values, use the arrow keys to move to the yStat column and enter the y values.
- When all data has been entered, press Exit to clear the screen and exit the Stat menu.
Calculate the linear regression statistics. The correlation coefficient is a measure of how closely the data approximates a straight line. A graphing calculator with statistical functions can calculate the best fit line and correlation coefficient very quickly.
- Enter the Stat function and then press the Calc button. On the TI-86, this is [2nd] [Stat] [F1].
- Choose the Linear Regression Calculations. On the TI-86, this is [F3], labeled "LinR." The graphical display will then display the line "LinR _" with a blinking cursor.
- You must now enter the names of the two variables you want to calculate. These are xStat and yStat.
  - On the TI-86, select the name list ("Names") by pressing [2nd] [List] [F3].
  - The bottom line of your screen should now show the available variables. Choose [xStat] (this is probably the F1 or F2 button), then enter a comma and then [yStat].
  - Press Enter to calculate the data
Interpret the results. When you press Enter, the calculator will immediately calculate the following information for the data you entered:
- y=a+bX{ displaystyle y = a + bx}Understand the concept of correlation. Correlation refers to the statistical relationship between two quantities. The correlation coefficient is a single number that you can calculate for two sets of data points. The number is always something between -1 and +1, and indicates how closely the two data sets are.
  - For example, if you measured the height and age of children up to about 12 years old, you would expect to find a strong positive correlation. As kids get older, they tend to get taller.
  - An example of a negative correlation is comparing the time someone spends practicing golf with that person's golf score. As practice progresses, the score should drop.
  - Ultimately, you would expect little correlation, positive or negative, between a person's shoe size, for example, and their exam grades.
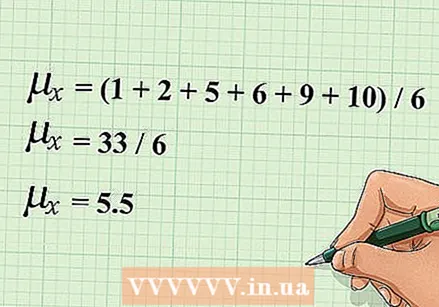- Calculate the mean. The arithmetic mean, or "mean", of a set of data is calculated by adding all the values of the data and then dividing by the number of values in the set. To determine the correlation coefficient for your data, you need to calculate the average of each set of data.
  - The mean of a variable is indicated by the variable with a horizontal line above it. This is often referred to as "x-bar" or "y-bar" for the data sets of x and y. Alternatively, the mean can be denoted by the lowercase Greek letter μ (mu). For example, to indicate the mean of data points of x, you could use μ_X or μ (x).
  - For example, if you have a set of x (1,2,5,6,9,10), then the average of this data is calculated as follows:
    - μX=(1+2+5+6+9+10)/6{ displaystyle mu _ {x} = (1 + 2 + 5 + 6 + 9 + 10) / 6}Know the importance of the standard deviation. In statistics, the standard deviation measures the variation, showing the dispersion of the numbers from the mean. A group of numbers with a low standard deviation is quite close to each other. A group of numbers with a high standard deviation is more scattered.
      - As a symbol, the standard deviation is expressed using the lowercase letter s or the Greek letter σ (sigma). Thus, the standard deviation of the x data is written as s_X or σ_X.
    - Recognize the summation notation. The summation operator is one of the most common operators in mathematics, and it indicates a sum of values. It is represented by the Greek capital letter, sigma or ∑.
      - For example, if you have a collection of data points x (1,2,5,6,9,10), then ∑x means:
        1+2+5+6+9+10 = 33

Tips

The correlation coefficient is sometimes referred to as the "Pearson product-moment correlation coefficient" in honor of Karl Pearson, its developer.
In general, a correlation coefficient higher than 0.8 (positive or negative) represents a strong correlation; a correlation coefficient lower than 0.5 (positive or negative again) represents a weak correlation coefficient.

Warnings

Correlation shows that two data sets are connected in some way. However, be careful not to interpret this as a causal relationship. For example, if you compare people's shoe sizes and their height, you will likely find a strong positive correlation. Taller people generally have bigger feet. However, this doesn't mean that getting tall will make your feet grow, or that big feet will make you grow tall. They just happen together.