Content

• To step
• Method 1 of 4: Using the area and length

There are numerous ways to find the missing dimensions of a rectangle, and the method you use depends on the data you have. As long as the area or perimeter is known, as well as the length of one side of the rectangle (or the ratio between the length and width), the missing dimension can be determined. The properties of a rectangle are such that these methods can be used to determine its width or length.

To step

Method 1 of 4: Using the area and length

1. Write down the formula for the area of ​​a rectangle. The formula is ${ displaystyle A = (l) (w)}$Use the area and length values ​​in the formula. Make sure to substitute for the correct variables.
   • For example, if you want to find the width of a rectangle with an area of ​​24 cm and a length of 8 cm, your formula would look like this:
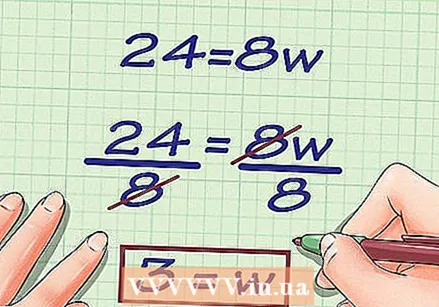     ${ displaystyle 24 = 8w}$Solve for w{ displaystyle w}Write down your final answer. Do not forget to state the unit of the measurement values.
     • For example, for a rectangle with an area of 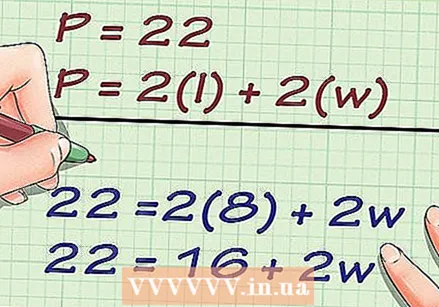${ displaystyle 24cm ^ {2}}$Use the circumference and length in the formula. Make sure to substitute for the correct variables.
       • For example, if you want to determine the width of a rectangle with a circumference of 22 cm and a length of 8 cm, the formula would look like this:
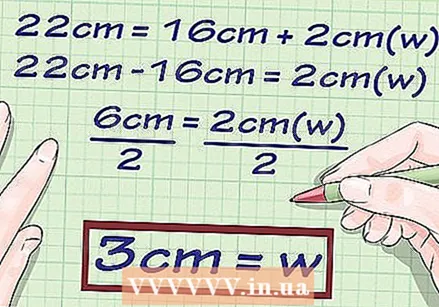         ${ displaystyle 22 = 2 (8) + 2w}$Solve w{ displaystyle w}Write down the final answer. Do not forget to state the unit of the measurement values.
         • For example, for a rectangle with an outline of ${ displaystyle 22cm}$Write down the formula for the diagonal of a rectangle. The formula is ${ displaystyle D = { sqrt {w ^ {2} + l ^ {2}}}}$Substitute the values ​​of the diagonal and side in the formula. Make sure to substitute for the correct variables.
           • For example, when determining the width of a rectangle with a diagonal of 5 cm and a side of 4 cm, the formula would look like this: ${ displaystyle 5 = { sqrt {w ^ {2} + 4 ^ {2}}}}$Square both sides of the formula. You need to do this to get rid of the square root sign so that isolating the width variable becomes easier.
             • For instance:
               ${ displaystyle 5 = { sqrt {w ^ {2} + 4 ^ {2}}}}$Isolate the variable w{ displaystyle w}Solve for w{ displaystyle w}Write down the final answer. Do not forget to state the unit of the measurement values.
               • For example, for a rectangle with a diagonal of ${ displaystyle 5cm}$Write down the formula for the area or perimeter of a rectangle. Which formula you use depends on the given measurement values. If the area is given, use the area formula. If the circumference is given, use the circumference formula.
                 • If the area or perimeter is unknown, or the relationship between the length and the width, you cannot use this method.
                 • The formula for the area is ${ displaystyle A = (l) (w)}$Write down the expression that describes the relationship between the length and the width. Write your expression in an equation with ${ displaystyle l}$Replace the variable l{ displaystyle l}Simplify the equation. The simplified equation can take different forms, depending on the relationship between the length and the width, and depending on whether you start from the area or the circumference. Try to compare with your ${ displaystyle w}$Solve for w{ displaystyle w}. Again, how you ${ displaystyle w}$ solves depends on the simplified equation. Use the basic rules of algebra and geometry to solve this.
                   • You may need to add or subtract to solve this, or factorize or use a quadratic equation to solve it.
                   • For instance, ${ displaystyle 0 = w ^ {2} + 5w-24}$ can be dissolved as follows:
                     ${ displaystyle 0 = w ^ {2} + 5w-24}$
                     ${ displaystyle 0 = (w + 8) (w-3)}$
                     You then have two possible solutions for this ${ displaystyle w}$: ${ displaystyle w = 3}$ or ${ displaystyle w = -8}$. Since a rectangle cannot have a negative width, you can exclude -8. So is your solution ${ displaystyle w = 3}$.