Content

• Steps
• Method 1 of 6: Cube
• Method 2 of 6: Rectangular prism / rectangular parallelepiped
• Method 3 of 6: Cylinder
• Method 4 of 6: Correct Pyramid
• Method 5 of 6: Cone
• Method 6 of 6: Ball

The volume of a figure is the three-dimensional space that the figure occupies. Imagine volume as the amount of liquid (or air, or sand) that can be filled in a given shape. Volume is measured in cubic units (mm, cm, m). This article will show you how to calculate the volume of six 3D shapes. You may notice that many of the volume formulas are similar, making them easier to remember.

Steps

Method 1 of 6: Cube

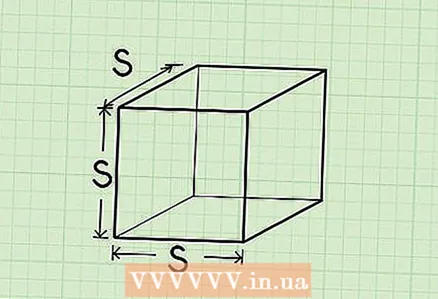1. 1 A cube is a three-dimensional shape that has six identical square faces, that is, all of its sides (edges) are equal.
   • For example, a die is a cube.
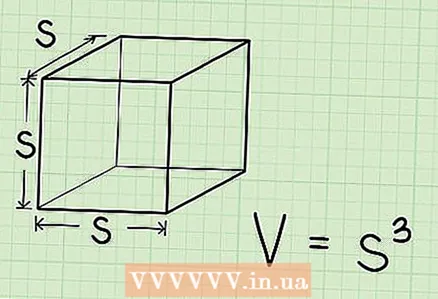2. 2 The formula for finding the volume of a cube:V = s, where V is the volume and s is the length of the rib.
   • Cubing is similar to the following multiplication: s = s * s * s
3. 3 Find the length of the side (edge) of the cube. It will be given in the problem or you need to measure it (with a ruler or tape measure). Since the edges of the cube are equal, measure any edge.
   • If you are not sure if your shape is a cube, measure each side to make sure they are equal. If they are not equal, skip to the next section.
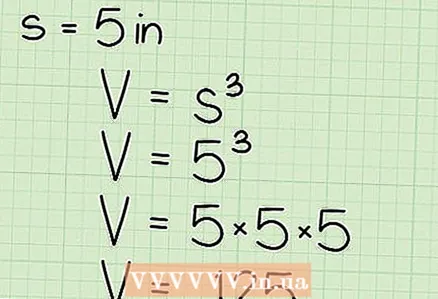4. 4 Substitute the length of the edge of the cube into the formula V = s. For example, if the edge of a cube is 5 cm, write the formula as follows: V = 5 = 5 * 5 * 5 = 125 cm is the volume of the cube.
5. 5 Be sure to add the appropriate units of measurement to your answer. In this example, the edge of the cube was measured in centimeters, so the volume will be measured in cubic centimeters. If, for example, the side of a cube is 3 cm, then V = 3 = 27 cm.

Method 2 of 6: Rectangular prism / rectangular parallelepiped

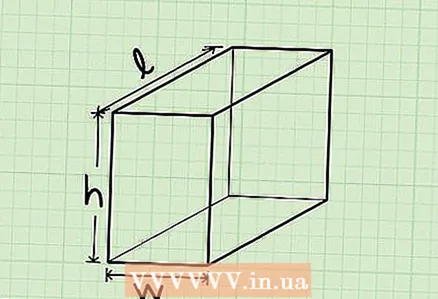1. 1 A rectangular parallelepiped or rectangular prism is a three-dimensional shape with six faces, each of which is a rectangle (think of a shoebox).
   • A cube is a special case of a rectangular parallelepiped in which all edges are equal.
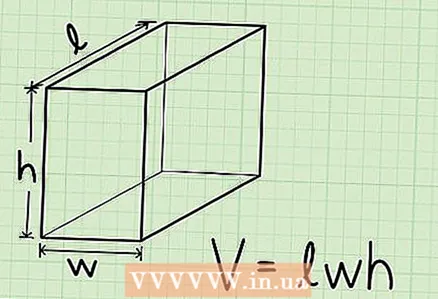2. 2 The formula for finding the volume of a rectangular parallelepiped or rectangular prism:V = l * w * hwhere V = volume, l = length, w = width, h = height.
3. 3 The length of a rectangular box is the longest edge of the top or bottom face, that is, the face the box is on (bottom face) or a parallel face (top face). The length will be given in the problem or you need to measure it (with a ruler or tape measure).
   • Example: the length of a rectangular parallelepiped is 4 cm, that is, l = 4 cm.
   • Don't worry about which ribs to choose for length, width and height. In any case, in the end you will get the correct answer (just measure three edges perpendicular to each other).
4. 4 The width of a rectangular box is the shortest edge of the top or bottom face, that is, the face on which the box stands (bottom face) or a parallel face (top face). The width will be given in the problem or you need to measure it (with a ruler or tape measure).
   • Example: the width of a rectangular parallelepiped is 3 cm, that is, w = 3 cm.
   • If you are measuring the edges of a box with a ruler or tape measure, be sure to measure them in the same units. Do not measure one edge in millimeters and the other in centimeters.
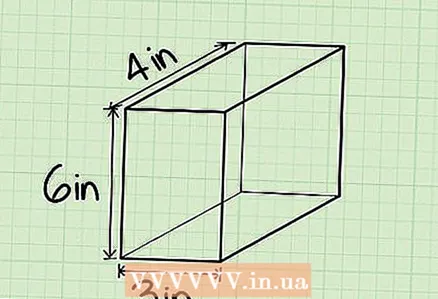5. 5 The height of a rectangular box is the distance between its bottom and top edges. The height will be given in the problem or you need to measure it (with a ruler or tape measure).
   • Example: the height of a rectangular parallelepiped is 6 cm, that is, h = 6 cm.
6. 6 Substitute the found values ​​into the formula V = l * w * h.
   • In our example, l = 4, w = 3 and h = 6. Therefore, V = 4 * 3 * 6 = 72.
7. 7 Be sure to add the appropriate units of measurement to your answer. In this example, the ribs were measured in centimeters, so the volume will be measured in cubic centimeters: 72 cm.
   • If in a rectangular prism l = 2 cm, w = 4 cm, h = 8 cm, then V = 2 * 4 * 8 = 64 cm

Method 3 of 6: Cylinder

1. 1 A cylinder is a three-dimensional shape bounded by a cylindrical surface and two parallel planes that intersect it.
   • For example, an AA bank or battery is shaped like a cylinder.
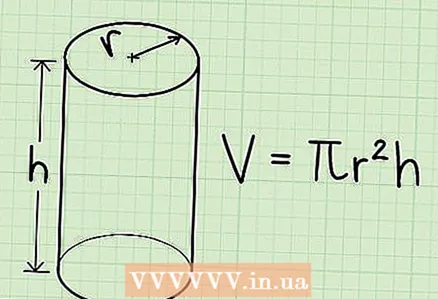2. 2 The formula for finding the volume of a cylinder:V = πrh, where V is the volume, h is the height, r is the radius of the base, and πr is the area of ​​the base of the cylinder.
   • In some problems, the answer is required to be presented with pi, and in some, instead of pi, substitute 3.14.
   • The formula for finding the volume of a cylinder is actually very similar to the formula for calculating the volume of a rectangular prism, that is, you multiply the height and area of ​​the base. In a rectangular prism, the base area is l * w, and in a cylinder it is πr.
3. 3 Find the radius of the base. It is most likely given in the problem. If given a diameter, divide it by 2 to find the radius (d = 2r).
4. 4 If no radius is given, measure it. To do this, measure the base of the cylinder with a ruler or tape measure. Measure the base at its widest point (that is, measure the base diameter) and then divide this value by 2 to find the radius.
   • Another option is to measure the circumference of the cylinder (that is, measure the circumference of the cylinder) using a tape measure, and then find the radius using the formula r = c / 2π, where c is the circumference (circumference) of the cylinder (2π = 6.28).
   • For example, if the girth of the cylinder is 8 cm, then the radius will be 1.27 cm.
   • If you need an accurate measurement, you can use both methods to make sure the radius values ​​match (finding the radius through the circumference is more accurate).
5. 5 Calculate the area of ​​the round base. To do this, plug the radius into the πr formula.
   • If the radius of the base is 4 cm, then the area of ​​the base is π4.
   • 4 = 4 * 4 = 16.16 * π = 16 * 3.14 = 50.24 cm
   • If the diameter of the base is given, then remember that d = 2r. You need to halve the diameter to find the radius.
6. 6 Find the height of the cylinder. This is the distance between two round bases. The height will be given in the problem or you need to measure it (with a ruler or tape measure).
7. 7 Multiply the area of ​​the base by the height of the cylinder to find its volume. Alternatively, simply plug in the values ​​of the corresponding quantities into the formula V = πrh. In our example, when the base radius is 4 cm and the height is 10 cm:
   • V = π410
   • π4 = 50,24
   • 50,24 * 10 = 502,4
   • V = 502.4
8. 8 Be sure to add the appropriate units of measurement to your answer. In the example given, all quantities were measured in centimeters, so the volume will be measured in cubic centimeters: 502.4 cm.

Method 4 of 6: Correct Pyramid

1. 1 A pyramid is a three-dimensional shape with a polygon at its base, and the faces are triangles with a common vertex. A regular pyramid is a three-dimensional shape with a regular polygon at its base (with equal sides), and the top is projected to the center of the base.
   • Usually we imagine a pyramid with a square base, but at the base of the pyramid there can be a polygon with 5, 6 or even 100 sides!
   • A pyramid with a round base is called a cone, which will be discussed in the next section.
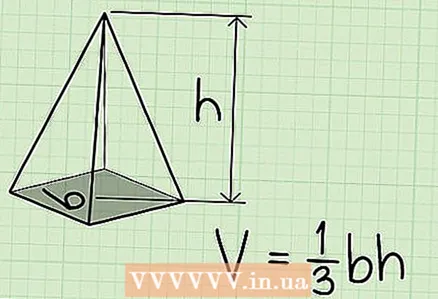2. 2 The formula for finding the volume of a regular pyramid:V = 1 / 3bh, where b is the area of ​​the base of the pyramid, h is the height of the pyramid (the perpendicular connecting the base and the top of the pyramid).
   • This formula for calculating the volume of a pyramid is equally valid for regular pyramids (in which the top is projected to the center of the base) and inclined (in which the top is not projected to the center of the base).
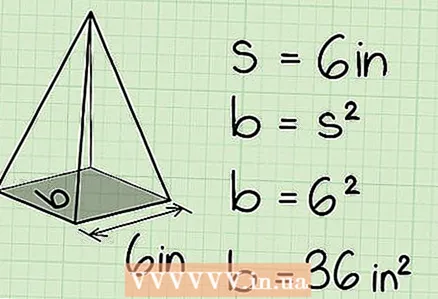3. 3 Calculate the area of ​​the base. The formula will depend on the shape at the base of the pyramid. In our example, at the base of the pyramid is a square with a side of 6 cm. The area of ​​the square is s, where s is the side of the square. Thus, in our example, the area of ​​the base of the pyramid is 6 = 36 cm
   • The area of ​​a triangle is 1 / 2bh, where h is the height of the triangle, b is the side to which the height is drawn.
   • The area of ​​any regular polygon can be calculated by the formula: A = 1 / 2pa, where A is the area, p is the perimeter of the figure, and a is the apothem (the segment connecting the center of the figure with the middle of either side of the figure). For more information on finding the area of ​​polygons read this article.
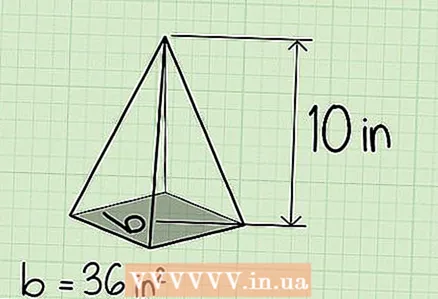4. 4 Find the height of the pyramid. The height will be given in the problem. In our example, the height of the pyramid is 10 cm.
5. 5 Multiply the area at the base of the pyramid by its height, and then divide the result by 3 to find the volume of the pyramid. Formula for calculating the volume of a pyramid: V = 1 / 3bh. In our example, the base area is 36 and the height is 10, so the volume is 36 * 10 * 1/3 = 120.
   • If, for example, a pyramid with a pentagonal base with an area of ​​26 is given, and the height of the pyramid is 8, then the volume of the pyramid is 1/3 * 26 * 8 = 69.33.
6. 6 Be sure to add the appropriate units of measurement to your answer. In the example given, all quantities were measured in centimeters, so the volume will be measured in cubic centimeters: 120 cm.

Method 5 of 6: Cone

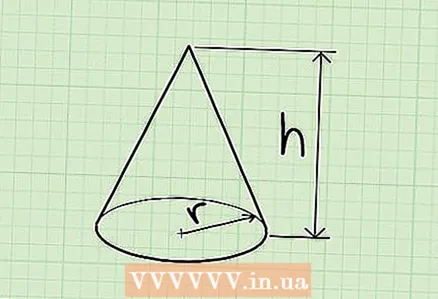1. 1 A cone is a three-dimensional shape that has a circular base and one vertex. Or a cone is a special case of a pyramid with a round base.
   • If the apex of the cone is directly above the center of the circular base, then the cone is called straight; otherwise, the cone is called oblique. But the formula for calculating the volume of a cone is the same for both types of cone.
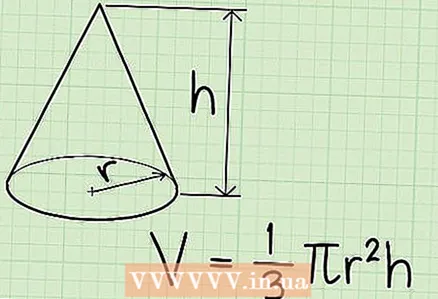2. 2 Formula for calculating the volume of a cone: V = 1 / 3πrh, where r is the radius of the round base, h is the height of the cone.
   • b = πr is the area of ​​the round base of the cone. Thus, the formula for calculating the volume of a cone can be written as follows: V = 1 / 3bh, which coincides with the formula for finding the volume of a pyramid!
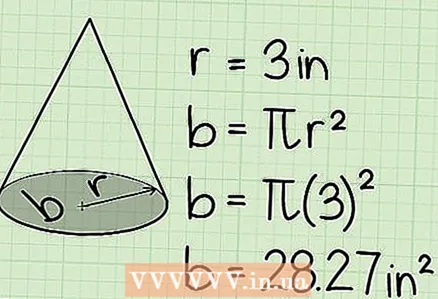3. 3 Calculate the area of ​​the round base. The radius must be given in the problem. If the diameter of the base is given, then remember that d = 2r. You need to halve the diameter to find the radius. To calculate the area of ​​a circular base, plug the radius into the πr formula.
   • For example, the radius of the round base of the cone is 3 cm. Then the area of ​​this base is π3.
   • π3 = π(3*3) = 9π.
   • = 28.27 cm
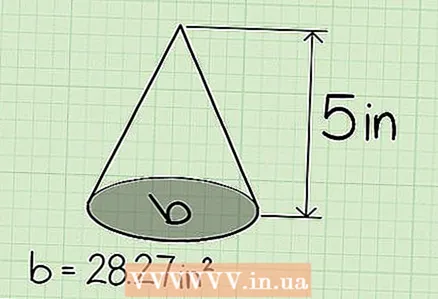4. 4 Find the height of the cone. This is a perpendicular drawn from the top to the base of the pyramid. In our example, the height of the cone is 5 cm.
5. 5 Multiply the height of the cone and the area of ​​the base. In our example, the base area is 28.27 cm and the height is 5 cm, so bh = 28.27 * 5 = 141.35.
6. 6 Now multiply your result by 1/3 (or just divide it by 3) to find the volume of the cone. In the above step, you found the volume of the cylinder, and the volume of the cone is always 3 times less than the volume of the cylinder.
   • In our example: 141.35 * 1/3 = 47.12 is the volume of the cone.
   • Or: 1 / 3π35 = 47.12
7. 7 Be sure to add the appropriate units of measurement to your answer. In the example given, all quantities were measured in centimeters, so the volume will be measured in cubic centimeters: 47.12 cm.

Method 6 of 6: Ball

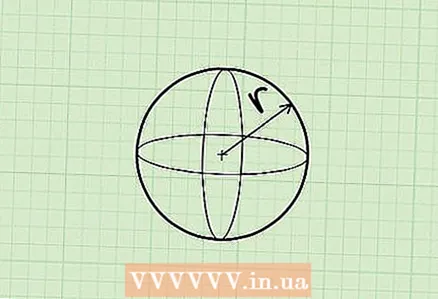1. 1 A ball is a perfectly circular three-dimensional shape, each point on the surface of which is equidistant from one point (the center of the ball).
2. 2 Formula for calculating the volume of a ball: V = 4 / 3πr, where r is the radius of the ball.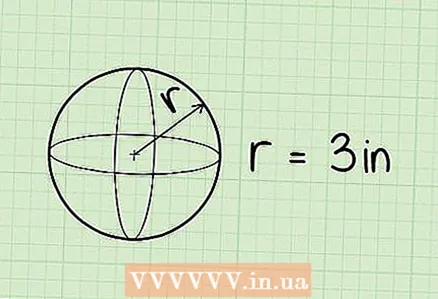
3. 3 Find the radius of the ball. The radius must be given in the problem. If the diameter of the ball is given, then remember that d = 2r. You need to halve the diameter to find the radius. For example, the radius of the ball is 3 cm.
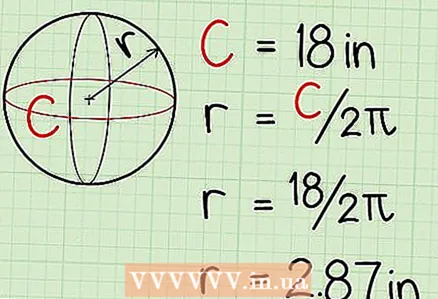4. 4 If no radius is given, calculate it. To do this, measure the circumference of a ball (such as a tennis ball) at its widest point using a piece of string, string, or similar object. Then measure the length of the rope to find the circumference. Divide this value by 2π (or 6.28) to find the radius of the ball.
   • For example, if you measured a ball and found its circumference to be 18 cm, divide that number by 6.28 to find the ball's radius to be 2.87 cm.
   • Take 3 measurements of the ball's circumference, and then average the values ​​obtained (add them and divide the sum by 3) to make sure you get a value close to true.
   • For example, as a result of three measurements of the circumference, you get the following results: 18 cm, 17.75 cm, 18.2 cm.Add these values: 18 + 17.5 + 18.2 = 53.95, and then divide them by 3 : 53.95 / 3 = 17.98. Use this average when calculating the volume of the ball.
5. 5 Cube the radius (r). That is, r = r * r * r. In our example, r = 3, so r = 3 * 3 * 3 = 27.
6. 6 Now multiply your result by 4/3. You can use a calculator or do the multiplication by hand and then simplify the fraction. In our example: 27 * 4/3 = 108/3 = 36.
7. 7 Multiply your result by π (3.14) to find the volume of the ball.
   • In our example: 36 * 3.14 = 113.09.
8. 8 Be sure to add the appropriate units of measurement to your answer. In the given example, all quantities were measured in centimeters, so the volume will be measured in cubic centimeters: 113.09 cm.