Content

• To step
• Method 1 of 5: Calculate Pi using a circle
• Method 2 of 5: Calculate Pi using infinite series
• Method 3 of 5: Calculating Pi using Buffon's Needle Problem
• Method 4 of 5: Calculate Pi with a limit
• Method 5 of 5: Arcsine and inverse sine function
• Tips

Pi (π) is one of the most important and fascinating numbers in mathematics. Simply represented as 3.14, it is used as a constant to calculate the circumference of a circle, using the radius or diameter. It is also an irrational number, which means that you can calculate it to an infinite number of decimal places without ever encountering a repeating pattern. This makes it difficult, but not impossible, to work accurately.

To step

Method 1 of 5: Calculate Pi using a circle

1. Make sure to use a perfect circle. This method will not work with an ellipse, oval, or anything other than a real circle. A circle is defined as all points in a plane that are equidistant from a given central point. Lids of, for example, a jam jar is a nice tool to use for this exercise. You can use this to roughly calculate a value of Pi. Even the thinnest, sharpest pencil is enormous compared to the accuracy required for an exact calculation of the number Pi.
2. Measure the circumference of the circle as accurately as you can. The circumference is the length of the entire circumference of the circle. Since this is going round and round, it can be a bit tricky to measure (that's why Pi is so important).
   • Lay a thread around the circumference, as precisely as possible. When the circle is complete, mark the wire, then measure the length of the wire with a ruler.
3. Measure the diameter of the circle. The diameter is the length of the diameter of a circle, through the center of the circle.
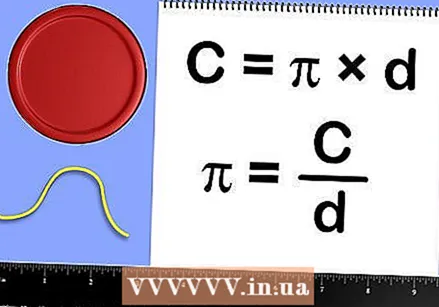4. Use the formula. The circumference of a circle can be found with the formula C = π * d = 2 * π * r. So pi is equal to the circumference of the circle divided by the diameter. Enter your numbers into a calculator: the result should be about 3.14.
5. For a more accurate result, repeat this process for several circles, then average the results. Your readings may not be perfect when it comes to an individual reading, but over time, averaging should be a really nice approximation of Pi.

Method 2 of 5: Calculate Pi using infinite series

1. Make use of the Gregory-Leibniz series. Mathematicians have found several mathematical sequences that, if followed indefinitely, can calculate Pi to an enormous number of decimal places. Some of these series are so complex that they require supercomputers to process them. One of the simplest, however, is the Gregory-Leibniz series. Maybe not very efficient, but it does return a more accurate number for pi with each iteration, eventually reaching 5 decimal places after 500,000 iterations. Here's the formula to use.
   • π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
   • Take 4 and subtract 4 divided by 3. Then add 4 divided by 5. Then subtract 4 divided by 7 again. Keep repeating this pattern with a numerator 4 and a consecutive odd number in the denominator. The more times you do this, the closer you get to pi.
2. Make use of the Nilakantha ranges. This is another infinite sequence that you can calculate pi with and is not difficult to understand. Although a bit more complicated, you can calculate pi much faster than with the Leibniz formula.
   • π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - 4/(12*13*14) ...
   • You apply this formula by first taking 2 and then alternately adding and subtracting fractions, using the numerator 4 and the denominator the product of 3 consecutive integers that increase with each new iteration. Each consecutive fraction starts with a series of integers where the first number in the series is the last number in the previous series (in the previous fraction). Even if you only do this a few times, you will soon get close to pi.

Method 3 of 5: Calculating Pi using Buffon's Needle Problem

1. Try the following experiment to calculate pi by throwing hot dogs. Pi also features in the thought experiment called Buffon's Needle Problem, which attempts to determine the likelihood that randomly thrown, uniform objects will land between or on a series of parallel lines on the floor. It turns out that if the distance between the lines equals the length of the thrown objects, the number of times the objects land on a line after throwing many times can be used to calculate pi.
   • Scientists and mathematicians have not yet discovered a way to calculate pi exactly, because they have not yet found a material so thin that you can perform exact calculations with it.

Method 4 of 5: Calculate Pi with a limit

1. Choose a large number. The larger the number, the more accurate your calculation will be.
2. Use the number, which we will call x, in this formula to calculate pi:x * sin (180 / x). For this to work, make sure your calculator is set to degrees. The reason this is called a limit is that its result is "limited" to pi. As you increase your number x, the result gets closer and closer to the value of pi.

Method 5 of 5: Arcsine and inverse sine function

1. Choose a number between -1 and 1. This is because the arcsine is not defined for numbers greater than 1 or less than -1.
2. Use the number in the following formula and the result will be roughly equal to pi.
   • pi = 2 * (Arcsin (sqrt (1 - x ^ 2))) + abs (Arcsin (x)).
     • Arcsin refers to an inverse sine in radians
     • Sqrt is an abbreviation for the square root of
     • Abs is short for absolute value
     • x ^ 2 is a certain power, in this case x squared.

Tips

• Calculating pi is fun and challenging, but calculating too many decimal places will not increase its usefulness Astronomers say it takes no more than 39 decimal places for the number pi to do highly accurate calculations .